题目内容
△ABC为等边三角形,D为射线BC上一点,∠ADE=60°,DE与∠ACB的外角平分线交于点E.
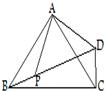
(1)如图1,点D在BC上,求证:CA=CD+CE;
(2)如图2,若D在BC的延长线上,直接写出CA、CD、CE之间的数量关系,

(1)如图1,点D在BC上,求证:CA=CD+CE;
(2)如图2,若D在BC的延长线上,直接写出CA、CD、CE之间的数量关系,

分析:(1)首先在AC上截取CM=CD,由△ABC为等边三角形,易得△CDM是等边三角形,继而可证得△ADM≌△EDC,即可得AM=EC,则可证得CA=CD+CE;
(2)首先在AC延长线上截取CM=CD,由△ABC为等边三角形,易得△CDM是等边三角形,继而可证得△ADM≌△EDC,即可得AM=EC,则可证得CA=CE-CD.
(2)首先在AC延长线上截取CM=CD,由△ABC为等边三角形,易得△CDM是等边三角形,继而可证得△ADM≌△EDC,即可得AM=EC,则可证得CA=CE-CD.
解答:证明:(1)在AC上截取CM=CD,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴△CDM是等边三角形,
∴MD=CD=CM,∠CMD=∠CDM=60°,
∴∠AMD=120°,
∵∠ADE=60°,
∴∠ADE=∠MDC,
∴∠ADM=∠EDC,
∵DE与∠ACB的外角平分线交于点E,
∴∠ACE=60°,
∴∠DCE=120°=∠AMD,
在△ADM和△EDC中,
,
 ∴△ADM≌△EDC(ASA),
∴△ADM≌△EDC(ASA),
∴AM=EC,
∴CA=CM+AM=CD+CE;
(2)CA=CE-CD.
证明:在AC的延长线上截取CM=CD,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠DCM=60°,
∴△CDM是等边三角形,
∴MD=CD=CM,∠CMD=∠CDM=60°,
∵DE与∠ACB的外角平分线交于点E,
∴∠ACE=∠DCE=60°,
∴∠ECD=∠AMD,
∵∠ADE=60°,
∴∠ADE=∠CDM,
∴∠ADM=∠EDC,
在△ADM和△EDC中,
,
∴△ADM≌△EDC(ASA),
∴AM=EC,
∴CA=AM-CM=CE-CD.
∵△ABC是等边三角形,
∴∠ACB=60°,
∴△CDM是等边三角形,
∴MD=CD=CM,∠CMD=∠CDM=60°,
∴∠AMD=120°,
∵∠ADE=60°,
∴∠ADE=∠MDC,
∴∠ADM=∠EDC,
∵DE与∠ACB的外角平分线交于点E,
∴∠ACE=60°,
∴∠DCE=120°=∠AMD,
在△ADM和△EDC中,
|
 ∴△ADM≌△EDC(ASA),
∴△ADM≌△EDC(ASA),∴AM=EC,
∴CA=CM+AM=CD+CE;
(2)CA=CE-CD.
证明:在AC的延长线上截取CM=CD,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠DCM=60°,
∴△CDM是等边三角形,
∴MD=CD=CM,∠CMD=∠CDM=60°,
∵DE与∠ACB的外角平分线交于点E,
∴∠ACE=∠DCE=60°,
∴∠ECD=∠AMD,
∵∠ADE=60°,
∴∠ADE=∠CDM,
∴∠ADM=∠EDC,
在△ADM和△EDC中,
|
∴△ADM≌△EDC(ASA),
∴AM=EC,
∴CA=AM-CM=CE-CD.
点评:此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 16、如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=
16、如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=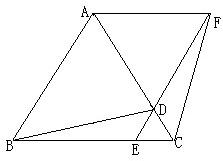 25、如图,△ABC为等边三角形,D、E为AC和BC边上的两点,且CD=CE,连接ED并延长到F,使AD=DF,连接AF、BD、CF,
25、如图,△ABC为等边三角形,D、E为AC和BC边上的两点,且CD=CE,连接ED并延长到F,使AD=DF,连接AF、BD、CF, 25、如图,已知△ABC为等边三角形,CF∥AB,点P为线段AB上任意一点(点P不与A、B重合),过点P作PE∥BC,分别交AC、CF于G、E.
25、如图,已知△ABC为等边三角形,CF∥AB,点P为线段AB上任意一点(点P不与A、B重合),过点P作PE∥BC,分别交AC、CF于G、E. 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1.
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1. 如图所示,△ABC为等边三角形,BD平分∠ABC,DE⊥BC于E,EC=1,则BC=
如图所示,△ABC为等边三角形,BD平分∠ABC,DE⊥BC于E,EC=1,则BC=