题目内容
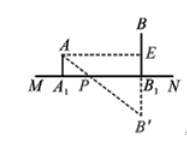
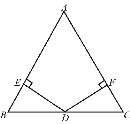
【题目】如图,在△ABC中,AC>AB,AD平分∠BAC,点D到点B与点C的距离相等,过点D作DE⊥BC于点E.
(1)求证:BE=CE;
(2)请直接写出∠ABC,∠ACB,∠ADE三者之间的数量关系;
(3)若∠ACB=40°,∠ADE=20°,求∠DCB的度数.

【答案】(1)见解析;(2)∠ABC-∠ACB=2∠ADE,理由见解析;(3)30°
【解析】
(1)利用等腰三角形底边上三线合一即可证明.
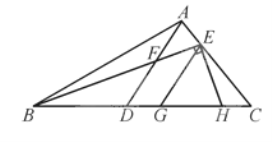
(2)结论:∠ABC-∠ACB=2∠ADE.如图2中,作BN⊥AD于N,交AC于M.证出∠ABN=∠AMN,再由角的和差求得。
(3)如图3中,作DM⊥AC于M,DN⊥AB于N.首先证明△DBN≌△DCM,推出∠BDN=∠CDM,推出∠CDB=∠MDN,由∠CAB+∠MDN=180°,推出∠CDB+∠CAB=180°,
利用(2)的结论求出∠ABC,∠CAB即可解决问题.
(1)证明:如图1中,
∵DB=DC,DE⊥BC,
∴CE=BE(等腰三角形底边上三线合一).
(2)结论:∠ABC-∠ACB=2∠ADE.
理由:如图2中,作BN⊥AD于N,交AC于M.
∵∠BAN=∠MAN,∠BAN+∠ABN=90°,∠MAN+∠AMN=90°,
∴∠ABN=∠AMN,
∵∠DOE=∠BON,∠DEO=∠BNO=90°,
∴∠EDA=∠CBM,
∴∠ABC-∠ACB=∠ABM+∠CBM-∠ACB=∠AMB+∠CBM-∠ABC=∠MCB+∠CBM+∠CBM-∠ACB=2∠CBN=2∠EDA.
故答案为∠ABC-∠ACB=2∠ADE
(3)解:如图3中,作DM⊥AC于M,DN⊥AB于N.
∵∠DAN=∠DAM,DM⊥AC,DN⊥AB,
∴DM=DN,
在Rt△DBN和Rt△DCM中,![]() ,
,
∴△DBN≌△DCM,
∴∠BDN=∠CDM,
∴∠CDB=∠MDN,
∵∠CAB+∠MDN=180°,
∴∠CDB+∠CAB=180°,
∵∠ACB=40°,∠ADE=20°,∠ABC-∠ACB=2∠ADE
∴∠ABC=80°,
∴∠CAB=180°-80°-40°=60°,
∴∠CDB=120°,
∴∠EDB=∠EDC=60°,
∴∠DCB=90°-∠EDC=30°.