题目内容
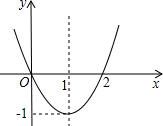 已知二次函数的图象如图所示,则
已知二次函数的图象如图所示,则
(1)这个二次函数的解析式是______;
(2)当x=______时,y=3
(3)当x的取值范围是______时,y>0.
解:(1)观察图象得:此函数的顶点坐标为(1,-1),对称轴为x=1,与x轴的交点坐标为(0,0),(2,0),
∴设此函数的解析式为y=a(x-1)2-1,
将点(0,0)代入函数解析式得a=1,
∴这个二次函数的解析式是y=(x-1)2-1,
即y=x2-2x;
(2)当x2-2x=3时,y=3,
解得x1=3,x2=-1,
∴当x=3或-1时,y=3;
(3)根据图象得,当x<0或x>2时,y>0.
分析:用待定系数法列三元一次方程组来求解.二次函数的解析式的一般式:y=ax2+bx+c(a,b,c是常数,a≠0).
点评:此题考查了学生的综合应用能力,解题的关键是准确识图.此题渗透了数形结合思想.在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解.
∴设此函数的解析式为y=a(x-1)2-1,
将点(0,0)代入函数解析式得a=1,
∴这个二次函数的解析式是y=(x-1)2-1,
即y=x2-2x;
(2)当x2-2x=3时,y=3,
解得x1=3,x2=-1,
∴当x=3或-1时,y=3;
(3)根据图象得,当x<0或x>2时,y>0.
分析:用待定系数法列三元一次方程组来求解.二次函数的解析式的一般式:y=ax2+bx+c(a,b,c是常数,a≠0).
点评:此题考查了学生的综合应用能力,解题的关键是准确识图.此题渗透了数形结合思想.在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 已知二次函数的图象如右图,则下列结论中,正确的结论有( )
已知二次函数的图象如右图,则下列结论中,正确的结论有( )①a+b+c>0 ②a-b+c<0 ③abc<0 ④b=2a ⑤b>0.
| A、5个 | B、4个 | C、3个 | D、2个 |
 14、已知二次函数的图象如图所示,那么此函数的解析式可能是( )
14、已知二次函数的图象如图所示,那么此函数的解析式可能是( )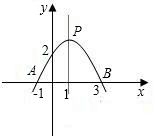 已知二次函数的图象如图所示,根据图中的数据,
已知二次函数的图象如图所示,根据图中的数据, 21、已知二次函数的图象如图所示,求它的解析式.
21、已知二次函数的图象如图所示,求它的解析式. 已知二次函数的图象如图所示,
已知二次函数的图象如图所示,