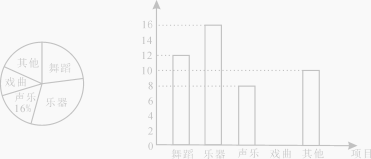
��Ŀ����
����Ŀ�������Ķ�����IJ��ϣ�����й����⣮
���ϣ���ѧϰ����ֵʱ����ʦ�̹����Ǿ���ֵ�ļ��κ��壬��|5��3|��ʾ5��3�������϶�Ӧ������֮��ľ��룻|5+3|=|5������3��|������|5+3|��ʾ5����3�������϶�Ӧ������֮��ľ��룻|5|=|5��0|������|5|��ʾ5�������϶�Ӧ�ĵ㵽ԭ��ľ��룮һ��أ���A��B�������Ϸֱ��ʾ������a��b����ôA��B֮��ľ���ɱ�ʾΪ|a��b|��
���⣨1������A��B��C�������Ϸֱ��ʾ��������5����1��3����ôA��B�ľ�������������������
A��C�ľ��������� ������. ��ֱ�������������
���⣨2������A��B��C�������Ϸֱ��ʾ������x����2��1����ôA��B�ľ�����A��C�ľ���֮�Ϳɱ�ʾΪ������ �� �������ú�����ֵ��ʽ�ӱ�ʾ����
���⣨3������������̽�������ҳ�����|x��3|+|x+1|=6��x������ֵ������ �� ��������
����|x��3|+|x+1|=p����x��ֵȡ�ڲ�С�ک�1�Ҳ�����3�ķ�Χʱ��p��ֵ�Dz���ģ�������p����Сֵ�������Сֵ������������������x��ֵȡ���������� �����ķ�Χʱ��|x|+|x��2|����Сֵ����������������
���⣨4������|x��3|+|x��2|+|x+1|����Сֵ�Լ���ʱx��ֵ.
���𰸡���1��4,8��2��|x����-2��|+|x��1|��|x+2|+|x��1|��3����-2��4��4��
����������������� ![]()
![]() ��
��![]() �ľ�����
�ľ�����![]()
![]() ��
��![]() �ľ�����
�ľ�����![]()
![]() �������⣺
�������⣺ ![]() ��
��![]() �ľ�����
�ľ�����![]() ��
��![]() �ľ���֮�ͱ�ʾΪ��
�ľ���֮�ͱ�ʾΪ�� ![]() ��
��![]() .
.
![]() ��
��![]() ��ʾ
��ʾ![]() ����
����![]() �͵�
�͵�![]() ����֮�͵���
����֮�͵���![]() .��������֮��ľ��빫ʽ�����ɽ����.�ڿ����ڲ�С��
.��������֮��ľ��빫ʽ�����ɽ����.�ڿ����ڲ�С��![]() �Ҳ�����
�Ҳ�����![]() �ķ�Χ����ȡһ���������������Сֵ.
�ķ�Χ����ȡһ���������������Сֵ.
![]() �ڲ�С��
�ڲ�С��![]() �Ҳ�����
�Ҳ�����![]() �ķ�Χ��ֵ���䣬��Сֵ�������Χ����ȡһ�������뼴��.
�ķ�Χ��ֵ���䣬��Сֵ�������Χ����ȡһ�������뼴��.
![]() Ҫʹ
Ҫʹ![]() |��ֵ��С
|��ֵ��С![]() ��ֵֻҪȡ
��ֵֻҪȡ![]() ��
��![]() ֮��(����
֮��(����![]() )������һ������Ҫʹ
)������һ������Ҫʹ![]() ��ֵ��С��
��ֵ��С�� ![]() Ӧȡ
Ӧȡ![]() ����Ȼ��
����Ȼ��![]() ʱ��ͬʱ����Ҫ��
ʱ��ͬʱ����Ҫ��![]() ����ԭʽ���㼴��.
����ԭʽ���㼴��.
�������:
![]()
![]()
![]() |��
|��![]() .
.
![]() ��
��![]() ��
��![]()
��![]() ����
��С��![]() �Ҳ�����
�Ҳ�����![]() ��
��![]()
��4����Ϊ����С��![]() �Ҳ�����
�Ҳ�����![]() ʱ
ʱ![]() ����Сֵ��
����Сֵ��![]()
���Ե�![]() ��Сʱ
��Сʱ![]() ����Сֵ.
����Сֵ.
���Ե�![]() ʱ����
ʱ����![]() ʱ
ʱ![]() ����Сֵ
����Сֵ![]()

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ijУΪ���˽����꼶ѧ����ѧϰ�����������꼶��ȡ��50��ѧ����ij�ν����˲��ԡ������õijɼ����ɼ���Ϊ�������������������±���ʾ�������㻭��Ƶ���ֲ�ֱ��ͼ��Ƶ������ͼ�����ش����⣺
���� |
|
|
|
|
|
Ƶ�� | 0.04 | 0.04 | 0.16 | 0.34 | 0.42 |
![]() ��β��Լ�����60�֣��������ж��٣�
��β��Լ�����60�֣��������ж��٣�
![]() ���β�����50��ѧ���ɼ����������Ƕ��٣���90������Ϊ���㣬����90�֣�
���β�����50��ѧ���ɼ����������Ƕ��٣���90������Ϊ���㣬����90�֣�
![]() ����꼶��ѧ��ѧϰ�����Σ�
����꼶��ѧ��ѧϰ�����Σ�