题目内容
【题目】数学“综合与实践”课中，老师带领同学们来到娄底市郊区，测算如图所示的仙女峰的高度，李红盛同学利用已学的数学知识设计了一个实践方案，并实施了如下操作：先在水平地面A处测得山顶B的仰角∠BAC为38.7°，再由A沿水平方向前进377米到达山脚C处，测得山坡BC的坡度为1：0.6，请你求出仙女峰的高度（参考数据：tan38.7°≈0.8）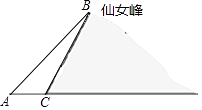
【答案】解：如图，过点B作BD⊥AC于点D，
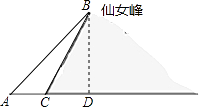
∵山坡BC的坡度为1：0.6，
∴ 
= 
，
则CD=0.6BD．
∵∠BAC为38.7°，
∴tan38.7°= 
= 
．
∵AC=377米，tan38.7°≈0.8，
∴ 
≈0.8，
解得BD=725（米）．
答：仙女峰的高度约为725米．
【解析】图中有两个直角三角形
BCD和ABD，先由坡度的定义：坡度=铅垂高度
水平距离，得出CD、BD的关系，在ABD中利用tan38.7°=
列出方程，求出BD.
【考点精析】关于本题考查的关于坡度坡角问题，需要了解坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA才能得出正确答案．
练习册系列答案
相关题目
