ΧβΡΩΡΎ»ί
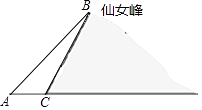
ΓΨΧβΡΩΓΩ[÷Σ Ε…ζ≥…]Ά®≥ΘΘ§”ΟΝΫ÷÷≤ΜΆ§ΒΡΖΫΖ®ΦΤΥψΆ§“ΜΗωΆΦ–ΈΒΡΟφΜΐΘ§Ω…“‘ΒΟΒΫ“ΜΗωΚψΒ» Ϋ.άΐ»γΘΚ»γΆΦΔΌ «“ΜΗω≥ΛΈΣ![]() Θ§ΩμΈΣ
Θ§ΩμΈΣ![]() ΒΡ≥ΛΖΫ–ΈΘ§―ΊΆΦ÷––ιœΏ”ΟΦτΒΕΨυΖ÷≥…ΥΡΗω–Γ≥ΛΖΫ–ΈΘ§»ΜΚσΑ¥ΆΦΔΎΒΡ–ΈΉ¥Τ¥≥…“ΜΗω’ΐΖΫ–ΈΘ°«κΫβ¥πœ¬Ν–Έ ΧβΘΚ
ΒΡ≥ΛΖΫ–ΈΘ§―ΊΆΦ÷––ιœΏ”ΟΦτΒΕΨυΖ÷≥…ΥΡΗω–Γ≥ΛΖΫ–ΈΘ§»ΜΚσΑ¥ΆΦΔΎΒΡ–ΈΉ¥Τ¥≥…“ΜΗω’ΐΖΫ–ΈΘ°«κΫβ¥πœ¬Ν–Έ ΧβΘΚ
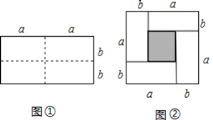
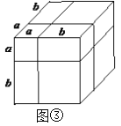
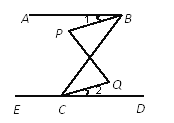
Θ®1Θ©ΆΦΔΎ÷–“θ”Α≤ΩΖ÷ΒΡ’ΐΖΫ–ΈΒΡ±Ώ≥Λ «________________;
Θ®2Θ©«κ”ΟΝΫ÷÷≤ΜΆ§ΒΡΖΫΖ®«σΆΦΔΎ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘΚ
ΖΫΖ®1:________________________ΘΜΖΫΖ®2ΘΚ_______________________;
Θ®3Θ©Ιέ≤λΆΦΔΎΘ§«κΡψ–¥≥ω![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ÷°ΦδΒΡΒ»ΝΩΙΊœΒ «__________;
÷°ΦδΒΡΒ»ΝΩΙΊœΒ «__________;
Θ®4Θ©ΗυΨίΘ®3Θ©÷–ΒΡΒ»ΝΩΙΊœΒΫβΨω»γœ¬Έ ΧβΘΚ»τ![]() ,
,![]() ,‘ρ
,‘ρ![]() =________;
=________;
[÷Σ Ε«®“Τ]
άύΥΤΒΊΘ§”ΟΝΫ÷÷≤ΜΆ§ΒΡΖΫΖ®ΦΤΥψΆ§“ΜΦΗΚΈΧεΒΡΧεΜΐΘ§“≤Ω…“‘ΒΟΒΫ“ΜΗωΚψΒ» Ϋ.
Θ®5Θ©ΗυΨίΆΦΔέΘ§–¥≥ω“ΜΗω¥ζ ΐΚψΒ» ΫΘΚ____________________________;
Θ®6Θ©“―÷Σ![]() Θ§
Θ§![]() Θ§άϊ”Ο…œΟφΒΡΙφ¬…«σ
Θ§άϊ”Ο…œΟφΒΡΙφ¬…«σ![]() ΒΡ÷Β.
ΒΡ÷Β.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΘΜ
ΘΜ![]() ΘΜΘ®3Θ©
ΘΜΘ®3Θ©![]() ΘΜΘ®4Θ©25
ΘΜΘ®4Θ©25
Θ®5Θ©![]() ΘΜΘ®6Θ©18.
ΘΜΘ®6Θ©18.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΆΦ–Έ÷–Θ§“θ”Α’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ–Γ≥ΛΖΫ–ΈΒΡ≥Λ”κΩμΒΡ≤νΘ§Φ¥Ω…«σΒΟ¥πΑΗΘΜ
Θ®2Θ©“άΨίΆΦ–ΈΒΡΧΊΒψΘ§Ζ÷ΈΣΝΫ÷÷ΖΫΖ®Θ§“Μ÷÷“άΨί±Ώ≥Λ‘Υ”ΟΟφΜΐΙΪ Ϋ÷±Ϋ”«σΟφΜΐΘ§Νμ“Μ÷÷”Ο¥σ’ΐΖΫ–ΈΒΡΟφΜΐΦθ»ΞΥΡΗω–ΓΨΊ–ΈΒΡΟφΜΐΘΜ
Θ®3Θ©ΗυΨίΝΫ÷÷ΟφΜΐΒΡ«σΖ®ΒΡΫαΙϊœύΒ»Θ§Φ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
Θ®4Θ©ΗυΨίΒΎ»ΐΈ ÷–“―÷ΣΒΡΒ» ΫΘ§ΫΪ ΐ÷ΒΖ÷±π¥ζ»κΘ§Φ¥Ω…«σΒΟ¥πΑΗ.
Θ®5Θ©ΖΫΖ®1ΘΚΗυΨί’ΐΖΫΧεΒΡΧεΜΐΙΪ ΫΘ§’ΐΖΫΧεΒΡ±Ώ≥ΛΒΡΝΔΖΫΨΆ «’ΐΖΫΧεΒΡΧεΜΐΘΜ
ΖΫΖ®2ΘΚ2Ηω’ΐΖΫΧεΚΆ6Ηω≥ΛΖΫΧεΒΡΧεΜΐΚΆΨΆ «¥σ≥ΛΖΫΧεΒΡΧεΜΐΘΜ
Θ®6Θ©ΗυΨίΘ®5Θ©÷–ΒΡΙΪ ΫΘ§±δ–ΈΫχ––«σΫβΦ¥Ω….
Θ®1Θ©ΆΦΔΎ÷–“θ”Α≤ΩΖ÷ΒΡ’ΐΖΫ–ΈΒΡ±Ώ≥Λ «![]() ΘΜ
ΘΜ
Θ®2Θ©![]() ΘΜ
ΘΜ![]()
Θ®3Θ©![]()
Θ®4Θ©![]() ,
,![]() ,
,
![]()
Ι ¥πΑΗΈΣΘΚ25
Θ®5Θ©![]()
Θ®6Θ©![]()