Question

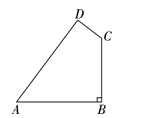
【题目】如图1，将三角板ABC与三角板ADE摆放在一起；如图2，其中∠ACB＝30°，∠DAE＝45°，∠BAC＝∠D＝90°．固定三角板ABC，将三角板ADE绕点A按顺时针方向旋转，记旋转角∠CAE＝α(0°＜α＜180°)．

(1)当α为　 　度时，AD∥BC，并在图3中画出相应的图形；

(2)在旋转过程中，试探究∠CAD与∠BAE之间的关系；

(3)当△ADE旋转速度为5°/秒时，且它的一边与△ABC的某一边平行(不共线)时，直接写出时间t的所有值．

Answer 1

【答案】（1）15，作图见解析；（2）在旋转过程中，与之间的关系为或；（3）所有符合要求的t的值为3秒或9秒或21秒或27秒或30秒．

【解析】

（1）先根据平行线的性质可求出，再根据角的和差即可得出的度数，然后画图即可；

（2）分、和三种情况，分别画出图形，根据角的和差即可得出结论；

（3）分五种情况，分别利用平行线的性质、角的和差求出旋转角的度数，从而可求出时间t的值．

（1）若

则

故答案为：15；

画图结果如下所示：

（2）依题意，分以下三种情况：

如图①，当时

则

如图②，当时

则

如图③，当时

则

综上，在旋转过程中，与之间的关系为或；

（3）依题意，分以下五种情况：

①当时

由（1）知，

则（秒）

②当时，此时，AD与AC重合

则，（秒）

③当时，此时，

则，（秒）

④当时，此时，AD与AB重合

则，（秒）

⑤当时

则，

（秒）

综上，所有符合要求的t的值为3秒或9秒或21秒或27秒或30秒．