题目内容
矩形的两条对角线的夹角为60°，这个矩形较短边与对角线的比是（ ）
| A．1∶1 | B．1∶2 | C．2∶3 | D．1∶ |
B
专题：计算题．
分析：根据矩形的两条对角线的夹角为60°，可以判定△AOB为等边三角形，即可求得AB=AO，在直角△ABC中，已知AC，AB，根据勾股定理即可计算BC的长，进而计算矩形的周长即可解题．
解答：解：
矩形的两条对角线的夹角为∠1=60°，
且矩形对角线相等且互相平分，
∴△AOB为等边三角形，
∴AB=AO=
AC，故选B．
点评：本题考查了矩形对角线相等且互相平分的性质，等边三角形的判定，勾股定理在直角三角形中的运用，本题中根据勾股定理计算BC的长是解题的关键．
练习册系列答案
应用题作业本系列答案
相关题目
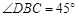，DE⊥BC于E，BF⊥CD于F，DE、BF相交于H，BF、AD的延长线相交于G，下列结论：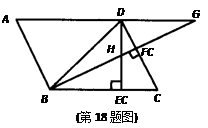
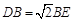；②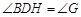
；③AB = BH；④
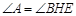；⑤BH = HG．
，这个正方形原来的边长是（ ）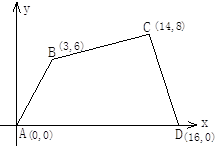
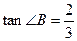.求BC的长.
（
，
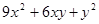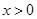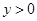）,利用分解因式，写出表示该正方形的边长的代数式