题目内容
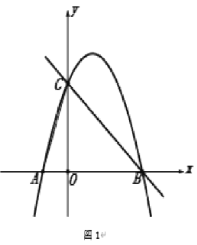
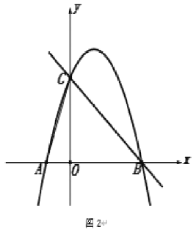
【题目】已知抛物线![]() 的最低点为 D(0,2)
的最低点为 D(0,2)
(1)求 m, n 的值
(2)直线 y=kx+4 交 y 轴于点 F,与抛物线交于 A,B 两点,直线 AD 交 x 轴于点 P.
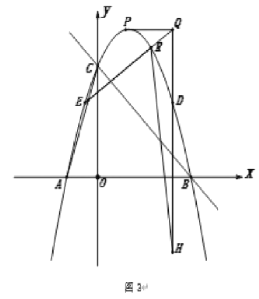
①求证:BP//y 轴
②作 BQ⊥AD 交 y 轴于点 Q,求证:对于每个给定的实数 k,四边形 FQPB 均为平行四边形
【答案】(1)m=0,n=2;(2)①见解析,②见解析.
【解析】
(1)抛物线![]() 的最低点为 D(0,2),根据对称轴求出m的值,再把D点代入解析式求出n的值;
的最低点为 D(0,2),根据对称轴求出m的值,再把D点代入解析式求出n的值;
(2)①联立 求出A点坐标,然后表示出P点的坐标,即可证明BP∥y轴;
求出A点坐标,然后表示出P点的坐标,即可证明BP∥y轴;
②BQ⊥AD和B点坐标,求出BQ的解析式,然后求出点Q的坐标,即可求出FQ的长度,证明FQ=BP,即可证明四边形 FQPB 为平行四边形.
(1)∵抛物线![]() 的最低点为 D(0,2),
的最低点为 D(0,2),
∴抛物线对称轴为x=0,
∴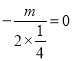 ,解得m=0,
,解得m=0,
把点D(0,2)代入抛物线![]() 中,
中,
则![]() ,解得n=2;
,解得n=2;
(2)①联立 ,解得
,解得![]() ,
,
把![]() 代入
代入![]() 中得:
中得:![]() ,
,
则A点坐标为:![]() ,
,
设AD直线解析式为![]() ,
,
把A![]() ,D(0,2)代入
,D(0,2)代入![]() 中,
中,
解得:![]() ,
,
令y=0,则![]() ,
,
则P点坐标为:![]() ,
,
∵B点横坐标为![]() ,
,
则BP∥y轴;
②设BQ的解析式为![]() ,
,
∵BQ⊥AD,
∴![]() ,
,
∵点B坐标为![]() ,
,
则BQ解析式为![]() ,
,
则Q点坐标为:![]()
则FQ=![]() ,
,
∴FQ=BP,
∵FQ∥BP,
∴四边形FQPB为平行四边形.


【题目】小明经过市场调查,整理出他妈妈商店里一种商品在第![]() 天的销售量的相关信息如下表:
天的销售量的相关信息如下表:
时间第 |
|
|
售价(元/件) |
| 50 |
每天销量(件) |
| |
已知该商品的进价为每件20元,设销售该商品的每天利润为![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.
【题目】某县教育局为了对该区八年级数学学科教学质量进行检查,对该区八年级的学生进行摸底,为了解摸底的情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:随机抽取![]() 学校与
学校与![]() 学校的各20名学生的数学成绩(单位:分)进行
学校的各20名学生的数学成绩(单位:分)进行
| 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
| 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据:按如下数据段整理、描述这两组数据
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
| 1 | 1 | 0 | 0 | 3 | 7 | 8 |
|
分析数据:两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
| 81.85 | 88 | 91 | 268.43 |
| 81.95 | 86 | m | 115.25 |
得出结论:
![]() :若
:若![]() 学校有800名八年级学生,估计这次考试成绩80分以上(包含80分)人数为多少人?
学校有800名八年级学生,估计这次考试成绩80分以上(包含80分)人数为多少人?
![]() :根据表格中的数据,推断出哪所学校学生的数学水平较高,并说明理由.(至少从两个不同的角度说明推断的合理性)
:根据表格中的数据,推断出哪所学校学生的数学水平较高,并说明理由.(至少从两个不同的角度说明推断的合理性)