��Ŀ����
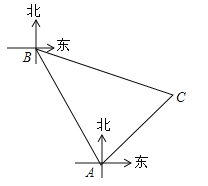
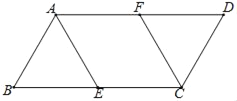
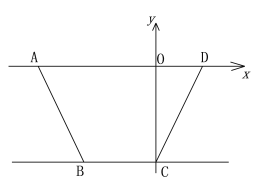
����Ŀ����ͼ����֪�ı���ABCD�У�AD��BC��BC=3����AD��x���ϣ���C��y���ϣ���D����Ϊ��2��0����ֱ��l��y=-2x-10������A��B.
��1�����ı���ABCD�������
��2����ֱ��l����ƽ�ƣ�ƽ�ƺ��ֱ����x�ύ�ڵ�P����ֱ��BC���ڵ�Q����AP=t.ֱ��l��ƽ�ƹ����У��Ƿ����t��ֵ��ʹ��PDQΪ���������Σ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��3����ֱ��l�Ƶ�A��ת����ֱ��l���ı���ABCD�������Ϊ1:3������ʱ����ֱ��д��l��BC�Ľ���M������.
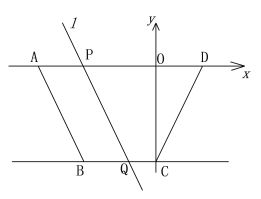
���𰸡���1��20����2�����ڣ�t=2��3��7��2![]() ����3��M1(-
����3��M1(-![]() ��-4)��M2(
��-4)��M2(![]() ��-4) ��
��-4) ��
��������
��1�����ݺ�������ʽ�õ�OA=5�����AD=7���õ�OC=4�����ǵõ����ۣ���2����Ҫ�������ۣ�Ҫʹ��PDQΪ���������Σ��������������м�����֤����3��ֱ��l���ı���ABCD�������Ϊ1:3������ʱ��Ҳ����Ҫ�������ۣ���ֱ��l��ಿ��������Ҳಿ�����=1:3����l�Ҳಿ���������ಿ�����=1:3���ٽ�����������ε��ж������ʣ�������������㼴�ɽ��.
�⣺��1����y=-2x-10�У���y=0ʱ��x=-5��
��A��-5��0����
��OA=5��
��AD=7��
��x=-3����y=-2x-10�ã�y=-4��
��OC=4��
���ı���ABCD�����=![]() ��3+7����4=20��
��3+7����4=20��
�ʴ�Ϊ��20��
��2�����ڣ��������£�
���ı���ABQP��ƽ���ı��Σ���PQ2=AB2=42+22=20��PD2=(7-t)2��DQ2=42+(5-t)2��
�ٵ�PQ2= PD2ʱ����20=(7-t)2��
��ã�t1=7+2![]() , t2=7-2
, t2=7-2![]() ;
;
�ڵ�PQ2= DQ2ʱ����20=42+(5-t)2��
��ã�t1=7����AD=7����t1=7ʱ��P,D���غϣ����������⣬��ȥ�� , t2=3;
�۵�PD2= DQ2ʱ����(7-t)2=42+(5-t)2��
��ã�t=2��
������������t=2��3��7��2![]() ʱ����PDQΪ���������Σ�
ʱ����PDQΪ���������Σ�
��3������ͼ������M���߶�BC��ʱ����ֱ��l��ಿ��������Ҳಿ�����=1:3��
��S��ABM=![]() S�ı���ABCD=5 ����OC=4����BM�ϵĸ�hBM=4,
S�ı���ABCD=5 ����OC=4����BM�ϵĸ�hBM=4,
��S��ABM=![]() ��BM��hBM=5����
��BM��hBM=5����![]() ��BM��4=5�����BM=
��BM��4=5�����BM=![]() ��
��
��CM=BC-BM=3-![]() =
=![]() ,
,
�֡�BC��x�ᣬC(0��-4)��M���ڵ������ޣ�
��M�������ΪM1(-![]() ��-4)��
��-4)��
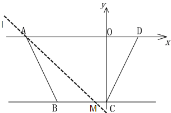
����ͼ����AD=7��OC=4�����ACD�����=7��4��2=14>5,
�൱ֱ��l�Ҳಿ���������ಿ�����=1:3ʱ����M���ڵ�C���Ҳ࣬���ʱAM��CD�Ľ���Ϊ��N����AND��AD�ߵĸ�ΪhAD����CNM��CM�ߵĸ�ΪhCM��
��ʱ��S��AND=![]() ��AD��hAD=5����
��AD��hAD=5����![]() ��7��hAD=5����ã�hAD=
��7��hAD=5����ã�hAD=![]() ��
��
��AD��CM��AD=7��OC=4�� CM�ϵĸ�hCM =4- ![]() =
=![]() �� ����AND����MNC��
�� ����AND����MNC��
��AD:CM= hAD: hCM,����7��CM=![]() :
:![]() ����ã�CM=
����ã�CM=![]() ,
,
��M�������ΪM1(![]() ��-4)��
��-4)��

����Ŀ��ɽ�����г�Խ��Խ�ܵ���ѧ����ϲ��������Ʒ�����Ͷ���г���ij���о�Ӫ��A�ͳ�ȥ�������ܶ�Ϊ5��Ԫ������ÿ�����ۼ۱�ȥ�꽵��400Ԫ����������������ͬ�������ܶ��ȥ�����20%��
��1������A�ͳ�ÿ���ۼ۶���Ԫ�������з��̵ķ������
��2���ó��мƻ��½�һ��A�ͳ����¿�B�ͳ���60������B�ͳ��Ľ�������������A�ͳ�������������Ӧ��ν�������ʹ������������ࣿ
A��B�����ͺų��Ľ��������ۼ۸����±���
A�ͳ� | B�ͳ� | |
�����۸�Ԫ�� | 1100 | 1400 |
���ۼ۸�Ԫ�� | ��������ۼ۸� | 2000 |