题目内容
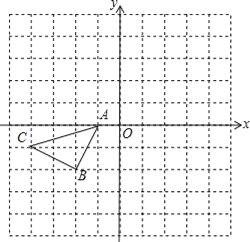
【题目】如图,矩形ABCD中,AB=10,BC=6,点E为CD边上一点。
(1)当AE平分∠BED时,求DE的长。
(2)你能把矩形ABCD沿某条直线剪一刀分成两块,再拼成一个菱形吗?如果能,在备用图中画出示意图,并计算菱形较长对角线的长。

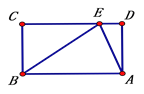
【答案】(1)2;(2)作图见解析.
【解析】整体分析:
(1)过点A作AF⊥BE,用面积法得BE=AB,在Rt△BCE中,用勾股定理求CE的长,即可求DE;(2)根据四边相等的四边形是菱形,沿BE剪一刀后,将△BCE向右边平移6个单位,构造直角三角形,用勾股定理求较长对角线的长.
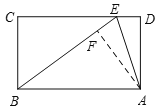
解:(1)如图,过点A作AF⊥BE,
∵AE平分∠BED,AD⊥DE,AF⊥EF,
∴AD=AF,
∵2S△EAB=AB×AD=BE×AF,
∴AB=BE,
∵AB=10,∴BE=10,
Rt△BCE中,BC=6,由勾股定理得CE=8.
∴DE=CD-CE=10-8=2.
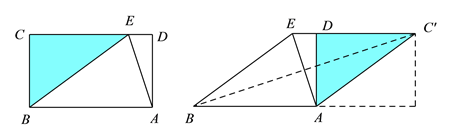
(2)如图,在矩形ABCD中,在CD边上取点E,使CE=8,则DE=2,
沿BE剪一切,则BE=10,再将△BCE向右平移6个单位长度,使BC与AD重合,所得四边形ABEC′即为菱形.
BC′=![]() =
=![]() =
=![]() .
.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目