��Ŀ����
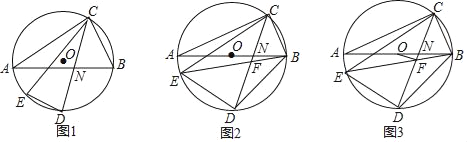
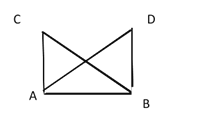
����Ŀ����ͼ�������������ĸ���A��B��C��D����A�������ϱ�ʾ������-12����D�������ϱ�ʾ������15�� AB��2����λ���ȣ�CD��1����λ���ȣ�
![]()
��1����B�������ϱ�ʾ������ ����C�������ϱ�ʾ������ ���߶�BC�� ��
��2������B��1����λ����/����ٶ������˶���ͬʱ��C��2����λ����/����ٶ������˶����˶�ʱ��Ϊt�룬��BC��6����λ���ȣ���t��ֵ��
��3�����߶�AB��1����λ����/����ٶ������˶���ͬʱ�߶�CD��2����λ����/����ٶ�Ҳ�����˶������˶�ʱ��Ϊt�룮
���ú���t��ʽ�ӷֱ��ʾ��A��B��C��D����A�� ��B�� ��C�� ��D�� ��
����0��t��24ʱ����MΪAC�е㣬NΪBD�е㣬������߶�MN�ij���
���𰸡���1��-10��14��24����2��6��10����3����-t-12��-t-10��14-2t��15-2t����![]() .
.
��������
��1������AB��CD�ij��Ƚ�ϵ�A��D�������ϱ�ʾ�����������ҳ���B��C�������ϱ�ʾ�������ٸ��������ľ��빫ʽ������߶�BC�ij��ȣ�
��2���ҳ��˶�ʱ��Ϊt��ʱ����B��C�������ϱ�ʾ���������������ľ��빫ʽ���BC=6�����ɵó�����t�ĺ�����ֵ���ŵ�һԪһ�η��̣���֮���ɵó����ۣ�
��3�����ҳ��˶�ʱ��Ϊt��ʱ�����ɵõ���A��B��C��D�������ϱ�ʾ������
���ɢ��еĴ���ʽ�����������ҳ���M��N�������ϱ�ʾ���������������ľ��빫ʽ����������߶�MN�ij���
�⣺��1����AB=2����A�������ϱ�ʾ������-12��
���B�������ϱ�ʾ������-10��
��CD=1����D�������ϱ�ʾ������15��
���C�������ϱ�ʾ������14��
��BC=14-��-10��=24��
�ʴ�Ϊ��-10��14��24��
��2�����˶�ʱ��Ϊt��ʱ����B�������ϱ�ʾ����Ϊt-10����C�������ϱ�ʾ����Ϊ��14-2t��
��BC=|t-10-��14-2t��|=|3t-24|��
��BC=6��
��|3t-24|=6��
��ã�t1=6��t2=10��
�൱BC=6����λ���ȣ�ʱ��t��ֵΪ6��10��
��3���ٵ��˶�ʱ��Ϊt��ʱ��
��A�������ϱ�ʾ����Ϊ��-t-12��
��B�������ϱ�ʾ����Ϊ��-t-10��
��C�������ϱ�ʾ����Ϊ��14-2t��
��D�������ϱ�ʾ����Ϊ��15-2t��
�ʴ�Ϊ��-t-12��-t-10��14-2t��15-2t��
�ڡ�0��t��24��
���Cһֱ�ڵ�B���Ҳ࣮
��MΪAC�е㣬NΪBD�е㣬
���M�������ϱ�ʾ����Ϊ��![]() ����N�������ϱ�ʾ����Ϊ��
����N�������ϱ�ʾ����Ϊ��![]() ��
��
��MN=![]() ��
��
�ʴ�Ϊ��![]() ��
��

 ���źþ���Ԫ����ĩ��ϵ�д�
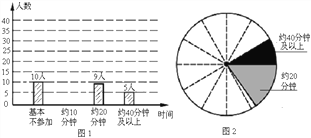
���źþ���Ԫ����ĩ��ϵ�д�����Ŀ��������ʵ�����Ϊ�˽�ȫУѧ����ѧ�ڲμ�������������ѧУ��������˱�У50��ѧ���μ�������Ĵ����������������õ������������£�
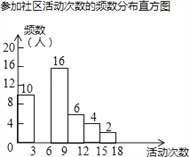
�μ������������Ƶ����Ƶ�ʷֲ���
�����x | Ƶ�� | Ƶ�� |
0��x��3 | 10 | 0.20 |
3��x��6 | a | 0.24 |
6��x��9 | 16 | 0.32 |
9��x��12 | 6 | 0.12 |
12��x��15 | m | b |
15��x��18 | 2 | n |
��������ͼ����Ϣ������������⣺
��1������a=������b=������
��2�����Ƶ���ֲ�ֱ��ͼ������������ͼ�����ע��Ӧ�����ݣ���
��3������У����1200��ѧ��������Ƹ�У����ѧ�ڲμ����������6�ε�ѧ���ж����ˣ�