题目内容
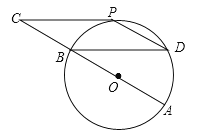
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 上的中线,
上的中线,![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,![]() ,垂足为
,垂足为![]() .
.
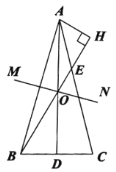
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
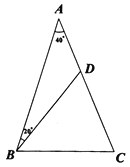
(3)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上的一点,且
上的一点,且![]() ,若
,若![]() ,请你直接写出
,请你直接写出![]() 的长.
的长.
【答案】(1)证明见解析 (2)![]() (3)
(3)![]()
【解析】
(1)根据题意利用中线的性质和垂直平分线的性质,即可解答.
(2)根据题意和由(1)得到![]() ,再利用勾股定理得到
,再利用勾股定理得到![]() ,最后利用全等三角形的性质,即可解答.
,最后利用全等三角形的性质,即可解答.
(3)作![]() 于
于![]() ,
,![]() 于
于![]() ,可得
,可得![]() ,设
,设![]() ,则
,则![]() ,利用勾股定理即可解答.
,利用勾股定理即可解答.
(1)证明:
∵![]() ,AD是
,AD是![]() 上的中线,
上的中线,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
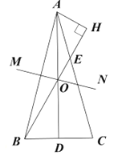
(2)解:∵![]() ,
,![]() 是
是![]() 上的中线,
上的中线,![]() ,
,
∴![]() .
.
由(1)知,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
由![]() ,及勾股定理,可得
,及勾股定理,可得![]() ,
,
∵![]() ,
,
∴![]() .
.
所以,![]() .
.
(3)![]() .
.
解:如图,
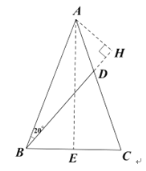
作![]() 于
于![]() ,
,![]() 于
于![]() ,仿(1)可得
,仿(1)可得![]() ,
,
且![]()
∴![]()
设![]() ,则
,则![]() ,在
,在![]() 中,
中,
![]() ,得,
,得,![]() (负值已舍).
(负值已舍).
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】成都华联商场经销甲、乙两种商品,甲种商品每件进价150元,售价200元;乙种商品每件进价350元,售价450元.
(1)该商场在“十一”黄金周期间销售甲、乙两种商品共100件,销售额为35000元,求甲、乙两种商品各销售了多少件?
(2)假若该商场在“十一”黄金周期间销售甲、乙两种商品进行如下优惠活动:
打折前一次性购物总金额 | 优惠措施 |
不超过3000元 | 不优惠 |
超过3000元且不超过4000元 | 总售价打九折 |
超过4000元 | 总售价打八折 |
按上述优惠条件,若小王第一天只购买甲种商品一次性付款2000元,第二天只购买乙种商品打折后一次性付款3240元,那么这两天他在该商场购买甲、乙两种商品一共多少件?