题目内容
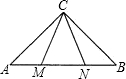如图，等腰直角三角形ABC中，顶点为C，∠MCN=45°，试说明△BCM∽△ANC．
解：∵△ACB是等腰直角三角形，
∴∠A=∠B=45°．
又∵∠MCN=45°，
∠CNA=∠B+∠BCN=45°+∠BCN，
∠MCB=∠MCN+∠NCB=45°+∠BCN．
∴∠CNA=∠MCB，
在△BCM和△ANC中，
，
∴△BCM∽△ANC．
分析：根据等腰直角三角形各底角为45°的性质，可以根据∠CNA=∠B+∠BCN=45°+∠BCN和∠MCB=∠MCN+∠NCB=45°+∠BCN即可求得∠CNA=∠MCB，即可求证△BCM∽△ANC，即可解题．
点评：本题考查了等腰直角三角形各底角为45°的性质，考查了相似三角形的判定，本题中求证∠CNA=∠MCB是解题的关键．
∴∠A=∠B=45°．
又∵∠MCN=45°，
∠CNA=∠B+∠BCN=45°+∠BCN，
∠MCB=∠MCN+∠NCB=45°+∠BCN．
∴∠CNA=∠MCB，
在△BCM和△ANC中，
，∴△BCM∽△ANC．
分析：根据等腰直角三角形各底角为45°的性质，可以根据∠CNA=∠B+∠BCN=45°+∠BCN和∠MCB=∠MCN+∠NCB=45°+∠BCN即可求得∠CNA=∠MCB，即可求证△BCM∽△ANC，即可解题．
点评：本题考查了等腰直角三角形各底角为45°的性质，考查了相似三角形的判定，本题中求证∠CNA=∠MCB是解题的关键．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
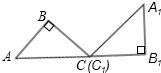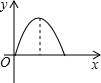
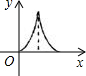
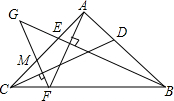
如图，等腰直角三角形ABC绕C点按顺时针旋转到△A1B1C1的位置（A、C、B1在同一直线上），∠B=90°，如果AB=1，那么AC运动到A1C1所经过的图形的面积是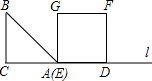
如图，等腰直角三角形ABC的腰长与正方形DEFG的边长相符，且边AC与DE在同一直线l上，△ABC从如图所示的起始位置（A、E重合），沿直线l水平向右平移，直至C、D重合为止．设△ABC与正方形DEFG重叠部分的面积为y，平移的距离为x，则y与x之间的函数关系大致是（ ）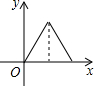
如图，等腰直角三角形ABC中，∠BAC=90°，D、E分别为AB、AC边上的点，AD=AE，AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M．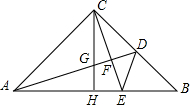
如图，等腰直角三角形△ABC中，∠ACB=90°，点D是BC的中点，CE⊥AD于点F交AB于点E，CH是AB上的高交AD于点G．
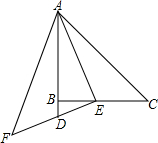如图，等腰直角三角形AEF的顶点E在等腰直角三角形ABC的边BC上．AB的延长线交EF于D点，其中∠AEF=∠ABC=90°．