题目内容
已知等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于O,∠ABD = 30°,AC⊥BC,AB =" 8" cm,则△COD的面积为( ).
A.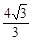 cm2 B.
cm2 B.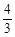 cm2 C.
cm2 C.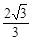 cm2 D.
cm2 D.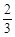 cm2
cm2
A.
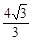 cm2 B.
cm2 B.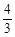 cm2 C.
cm2 C.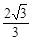 cm2 D.
cm2 D.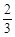 cm2
cm2A
解:∵梯形ABCD是等腰梯形,CD∥AB,
由SAS可证△DAB≌△CBA,
∴∠CAB=∠DCA=30°,
∵∠CAB=30°,又因为AC⊥BC,
∴∠DAB=∠CBA=60°,
∴∠DAC=∠DCA=30°,
∴CD=AD=BC=4cm,
∴AC2=AB2-BC2,
∴AC=4 cm,
cm,
∵梯形ABCD是等腰梯形,
∴AC=BD=4 cm,
cm,
∴S△ABC= ×4×4
×4×4 =8
=8 cm,
cm,
设DO为x,则CO=x,则AO=BO=(4 -x)cm,
-x)cm,
在Rt△COB中,CO2+BC2=BO2,
即:x2+42=(4 -x)2
-x)2
∴D0=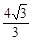 cm,
cm,
∴S△ADO= ×
×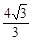 ×4=
×4= ,
,
∴S△AOB=S△ABC-S△ADO=
∵AB∥CD,
∴△AOB∽△DOC,
∴( )2=
)2=
∴S△DOC=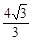 ,故选A
,故选A
由SAS可证△DAB≌△CBA,
∴∠CAB=∠DCA=30°,
∵∠CAB=30°,又因为AC⊥BC,
∴∠DAB=∠CBA=60°,
∴∠DAC=∠DCA=30°,
∴CD=AD=BC=4cm,
∴AC2=AB2-BC2,
∴AC=4
 cm,
cm,∵梯形ABCD是等腰梯形,

∴AC=BD=4
 cm,
cm,∴S△ABC=
 ×4×4
×4×4 =8
=8 cm,
cm,设DO为x,则CO=x,则AO=BO=(4
 -x)cm,
-x)cm,在Rt△COB中,CO2+BC2=BO2,
即:x2+42=(4
 -x)2
-x)2∴D0=
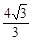 cm,
cm,∴S△ADO=
 ×
×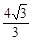 ×4=
×4= ,
,∴S△AOB=S△ABC-S△ADO=

∵AB∥CD,
∴△AOB∽△DOC,
∴(
 )2=
)2=
∴S△DOC=
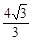 ,故选A
,故选A
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 ABCD中,∠DAB=60°,AB=2AD,点E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G。
ABCD中,∠DAB=60°,AB=2AD,点E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G。
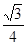 CG2;③若AF=2DF,则BG=6GF
CG2;③若AF=2DF,则BG=6GF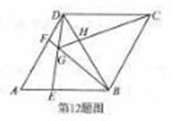
 .
. 等分点(靠近点A),
等分点(靠近点A),