题目内容
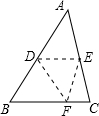 如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论:①△BDF是等腰三角形;②DE=
如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论:①△BDF是等腰三角形;②DE=| 1 |
| 2 |
| A、①③④ | B、②③④ |
| C、①②④ | D、①②③ |
分析:分别过点D、E作BC的垂线DG、EH;连接AF,由于折叠是轴对称图形知AF⊥DE,因为DE∥BC,所以AF⊥BC,且AM=MF,可以证明DE是△ABC的中位线.
由于折纸是轴对称图形知AD=DF,AE=EF,所以DA=DB=DF,可以证明①是等腰三角形;因DG∥AF∥EH,又因为DG是等腰三角形BDF的高,可证∠BDF=2∠DAM,同理∠CEF=2∠EAM,可证④正确;显然③四边形ADFE是菱形是错误的.
由于折纸是轴对称图形知AD=DF,AE=EF,所以DA=DB=DF,可以证明①是等腰三角形;因DG∥AF∥EH,又因为DG是等腰三角形BDF的高,可证∠BDF=2∠DAM,同理∠CEF=2∠EAM,可证④正确;显然③四边形ADFE是菱形是错误的.
解答: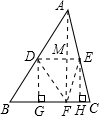 解:分别过点D、E作BC的垂线DG、EH;连接AF,
解:分别过点D、E作BC的垂线DG、EH;连接AF,
∵折叠是轴对称图形,∴AF⊥DE,
∵DE∥BC,∴AF⊥BC,且AM=MF,
∴D、E分别是AB、AC的中点,
即;②DE=
BC,正确.
∵AD=DF,AE=EF,
∴DA=DB=DF,∴①△BDF是等腰三角形,正确.
∵DG∥AF∥EH,∴∠BDG=∠DAM,
又∵DG是等腰三角形BDF的高,
∴∠BDF=2∠DAM,同理∠CEF=2∠EAM,
∴④∠BDF+∠FEC=2∠A;如图显然③四边形ADFE是菱形是错误的.
故选C.
 解:分别过点D、E作BC的垂线DG、EH;连接AF,
解:分别过点D、E作BC的垂线DG、EH;连接AF,∵折叠是轴对称图形,∴AF⊥DE,
∵DE∥BC,∴AF⊥BC,且AM=MF,
∴D、E分别是AB、AC的中点,
即;②DE=
| 1 |
| 2 |
∵AD=DF,AE=EF,
∴DA=DB=DF,∴①△BDF是等腰三角形,正确.
∵DG∥AF∥EH,∴∠BDG=∠DAM,
又∵DG是等腰三角形BDF的高,
∴∠BDF=2∠DAM,同理∠CEF=2∠EAM,
∴④∠BDF+∠FEC=2∠A;如图显然③四边形ADFE是菱形是错误的.
故选C.
点评:此题主要考查菱形的判定,等腰三角形的判定与性质的理解和掌握,轴对称图形等知识点,解答此题的关键是分别过点D、E作BC的垂线DG、EH;连接AF,然后分别求证各个结论,此题有一定的拔高难度,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
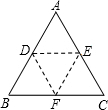 如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的是
如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的是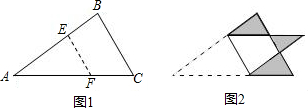
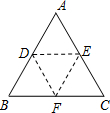 如图:将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )
如图:将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( ) 如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BDEC的外部时,∠1=72°,∠2=26°,则∠A=
如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BDEC的外部时,∠1=72°,∠2=26°,则∠A=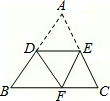 如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )
如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )