题目内容
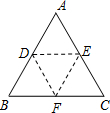 如图:将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )
如图:将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )①△BDF是等腰三角形;②DE=
| 1 |
| 2 |
分析:先根据折叠的性质得∠ADE=∠FDE,AD=FD,再根据平行线的性质得到∠ADE=∠B,∠FDE=∠BFD,则∠B=∠BFD,于是根据等腰三角形的判定可对①进行判断;由∠B=∠BFD得DB=DF,易得AD=DB,即D为AB的中点,可判断DE为△ABC的中位线,根据三角形中位线的性质可对②进行判断;同理可得∠C=∠EFC,
再根据三角形内角和定理得到∠BDF=180°-∠B-∠BFD=180°-2∠B,∠FEC=180°-∠C-∠EFC=180°-2∠C,则∠BDF+∠FEC=360°-2(∠B+∠C)=360°-2(180°-∠A)=2∠A,所以可对③进行判断;由于AD=DF,AE=EC,只有当AD=AE时,四边形ADFE是菱形,则要有△ABC为等腰三角形,而条件中没有△ABC为等腰三角形,则可对④进行判断.
再根据三角形内角和定理得到∠BDF=180°-∠B-∠BFD=180°-2∠B,∠FEC=180°-∠C-∠EFC=180°-2∠C,则∠BDF+∠FEC=360°-2(∠B+∠C)=360°-2(180°-∠A)=2∠A,所以可对③进行判断;由于AD=DF,AE=EC,只有当AD=AE时,四边形ADFE是菱形,则要有△ABC为等腰三角形,而条件中没有△ABC为等腰三角形,则可对④进行判断.
解答:解:∵三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,
∴∠ADE=∠FDE,AD=FD,
∵DE∥BC,
∴∠ADE=∠B,∠FDE=∠BFD,
∴∠B=∠BFD,
∴△BDF是等腰三角形,所以①正确;
∴DB=DF,
∴AD=DB,即D为AB的中点,
而DE∥BC,
∴DE为△ABC的中位线,
∴DE=
BC,所以②正确;
同理可得∠C=∠EFC,
∵∠BDF=180°-∠B-∠BFD=180°-2∠B,
∠FEC=180°-∠C-∠EFC=180°-2∠C,
∴∠BDF+∠FEC=360°-2(∠B+∠C)=360°-2(180°-∠A)=2∠A,所以③正确;
∵AD=DF,AE=EC,
∴当AD=AE时,四边形ADFE是菱形,此时△ABC为等腰三角形,
而△ABC不确定为等腰三角形,
∴不能判断四边形ADFE是菱形,所以④错误.
故选C.
∴∠ADE=∠FDE,AD=FD,
∵DE∥BC,
∴∠ADE=∠B,∠FDE=∠BFD,
∴∠B=∠BFD,
∴△BDF是等腰三角形,所以①正确;
∴DB=DF,
∴AD=DB,即D为AB的中点,
而DE∥BC,
∴DE为△ABC的中位线,
∴DE=
| 1 |
| 2 |
同理可得∠C=∠EFC,
∵∠BDF=180°-∠B-∠BFD=180°-2∠B,
∠FEC=180°-∠C-∠EFC=180°-2∠C,
∴∠BDF+∠FEC=360°-2(∠B+∠C)=360°-2(180°-∠A)=2∠A,所以③正确;
∵AD=DF,AE=EC,
∴当AD=AE时,四边形ADFE是菱形,此时△ABC为等腰三角形,
而△ABC不确定为等腰三角形,
∴不能判断四边形ADFE是菱形,所以④错误.
故选C.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了等腰三角形的判定、三角形内角和定理和菱形的判定.

练习册系列答案
相关题目
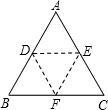 如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的是
如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的是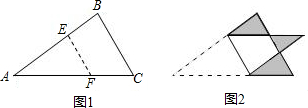
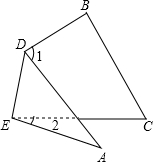 如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BDEC的外部时,∠1=72°,∠2=26°,则∠A=
如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BDEC的外部时,∠1=72°,∠2=26°,则∠A= 如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )
如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )