题目内容
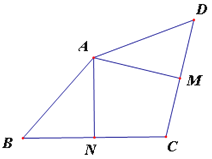
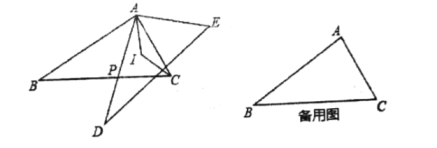
【题目】![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针旋转
按顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,
,![]() ,它们交于
,它们交于![]() 点,
点,
①求证:![]() .
.
②当![]() ,求
,求![]() 的度数.
的度数.
③当四边形![]() 是菱形时,求
是菱形时,求![]() 的长.
的长.

【答案】①证明见解析; ②![]() ;③
;③![]() .
.
【解析】
①先利用旋转的性质得AE=AB,AF=AC,∠EAF=∠BAC,则根据“SAS”证明△AEB≌△AFC,于是得到BE=CF;
②利用∠FAC=120°,AF=AC可得到∠ACF=30°,再利用AB=AC,∠BAC=45°得到∠ACB=67.5°,然后计算∠BCF;
③利用四边形ACDE是菱形得到AC∥DE,DE=AE=AC=1,则∠ABE=∠BAC=45°,于是可判断△ABE为等腰直角三角形,所以BE=![]() AB=
AB=![]() ,然后计算BE-DE即可.
,然后计算BE-DE即可.
解:①证明:∵![]() 绕点
绕点![]() 按顺时针方向旋转角
按顺时针方向旋转角![]() 得到
得到![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,即
,即![]() ,
,
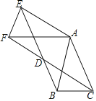
在![]() 和
和![]() 中,
中,
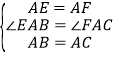 ,
,
∴![]() ,
,
∴![]() ;
;
②解:∵![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
③解:∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
【题目】甲、乙两班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如表,请根据表中数据解答下列问题
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
甲 | 1 | 1 | 1 | 4 | 0 | 3 |
乙 | 0 | 1 | 2 | 5 | 0 | 2 |
(1)分别写出甲、乙两班选手进球数的平均数、中位数与众数;
(2)如果要从这两个班中选出一个班级参加学校的投篮比赛,争取夺得总进球团体的第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?