题目内容
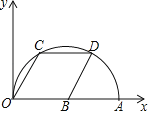
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点C、D在以OA为直径的半圆上,点B在OA上,且四边形OCDB是菱形,则点C的坐标为_________.
【答案】(![]() ,
,![]() )
)
【解析】
根据题意连接AD,延长DC交y轴于M,连接AC,则∠OMC=90°,由菱形的性质得出OB=OC=CD=BD,OC∥BD,CD∥OB,∠BOC=∠BDC,得出∠BOC=∠ABD=∠BDC,由圆的两条平行弦的性质得出![]() ,由圆周角定理得出∠ACO=90°,得出OC=AD=BD=CD,OC⊥AC,证明△ABD是等边三角形,得出AB=BD=OB,∠BOC=∠ABD=60°,得出OC=OB=
,由圆周角定理得出∠ACO=90°,得出OC=AD=BD=CD,OC⊥AC,证明△ABD是等边三角形,得出AB=BD=OB,∠BOC=∠ABD=60°,得出OC=OB=![]() OA=5,由直角三角形的性质得出CM=
OA=5,由直角三角形的性质得出CM=![]() OC=
OC=![]() ,OM=
,OM=![]() CM=
CM=![]() ,即可得出答案.
,即可得出答案.
解:连接AD,延长DC交y轴于M,连接AC,如图所示:
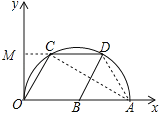
则∠OMC=90°,
∵四边形OCDB是菱形,
∴OB=OC=CD=BD,OC∥BD,CD∥OB,∠BOC=∠BDC,
∴∠BOC=∠ABD=∠BDC,
∵点C、D在以OA为直径的半圆上,CD∥OA,
∴![]() ,∠ACO=90°,
,∠ACO=90°,
∴OC=AD=BD=CD,OC⊥AC,
∴∠ABD=∠BAD,BD⊥AC,
∵CD=AD,
∴∠BDC=∠ADB,
∴∠ABD=∠BAD=∠ADB,
∴△ABD是等边三角形,
∴AB=BD=OB,∠BOC=∠ABD=60°,
∵点A的坐标是(10,0),
∴OA=10,
∴OC=OB=![]() OA=5,
OA=5,
∵∠OMC=90°,
∴∠COM=30°,
∴CM=![]() OC=
OC=![]() ,OM=
,OM=![]() CM=
CM=![]() ,
,
∴点C的坐标为(![]() ,
,![]() );
);
故答案为:(![]() ,
,![]() ).
).

【题目】已知函数![]() ,
,![]() ,探究函数图象和性质过程如下:
,探究函数图象和性质过程如下:
(1)下表是y与x的几组值,则解析式中的m= ,表格中的n= ;
x | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y |
|
|
| 1 |
| 3 |
| 4 |
| 3 | n | 0 | … |
(2)在平面直角坐标系中描出表格中各点,并画出函数图象:
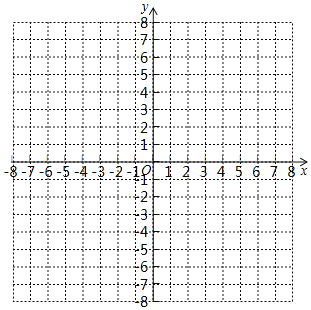
(3)若A(x1,y1)、B(x2,y2)、C(x3,y3)为函数图象上的三个点,其中x2+x3>4且﹣1<x1<0<x2<2<x3<4,则y1、y2、y3之间的大小关系是 ;
(4)若直线y=k+1与该函数图象有且仅有一个交点,则k的取值范围为 .
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.