Question

【题目】如图，直线y=﹣x+6分别交x轴、y轴于A、B两点，抛物线y=﹣x2+8，与y轴交于点D，点P是抛物线在第一象限部分上的一动点，过点P作PC⊥x轴于点C．

（1）点A的坐标为 ，点D的坐标为 ；

（2）探究发现：

①假设P与点D重合，则PB+PC= ；（直接填写答案）

②试判断：对于任意一点P，PB+PC的值是否为定值？并说明理由；

（3）试判断△PAB的面积是否存在最大值？若存在，求出最大值，并求出此时点P的坐标；若不存在，说明理由．

Answer 1

【答案】（1）（4，0），（0，8）；（2）①PB+PC=10；②是，见解析（3）△PAB的面积存在最大值，且最大值为13，此时点P的坐标为（6，）

【解析】

试题分析：（1）根据自变量与函数值的对应关系，可得答案；

（2）①根据线段的和差，可得PB，可得答案；

②根据勾股定理，可得PB的长，根据线段和差，可得答案；

（3）根据面积的和差，可得二次函数，根据二次函数的性质，可得最大值，根据自变量与函数值的对应关系，可得答案．

解：（1）y=﹣x+6当y=0时，x=4，即A（4，0），

y=﹣x2+8当x=0时，y=8，即D点坐标（0，8），

故答案为：（4，0），（0，8）；

（2）①PB=PO﹣OB=8﹣6=2，PB+PC=8+2=10；

②是，理由如下：

过点P作PQ⊥y轴于点Q，

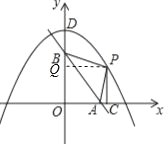
∵P在抛物线上，且在第一象限，

∴设P点坐标为（x，﹣x2+8）．

则PQ=x，PC=﹣x2+8．

当4≤x＜8时，PB===x2+2，

∴PB+PC=x2+2+（﹣x2）+8=10，

当0＜x＜4时，同理可得；

（3）存在．

设△PAB的面积为S．

由（2）假设．

当4≤x＜8时，有S=﹣﹣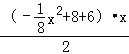

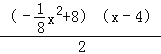
=﹣x2+3x+4=﹣（x﹣6）2+13．

当0＜x＜4时，s=﹣（x﹣6）2+13．

当x=6时，S最大=13，y=﹣×36+8=，

∴△PAB的面积存在最大值，且最大值为13，此时点P的坐标为（6，）