题目内容
【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.试说明△ABC是等腰三角形. 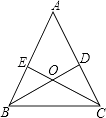
【答案】证明:∵OB=OC,
∴∠OBC=∠OCB,
∵锐角△ABC的两条高BD、CE相交于点O,
∴∠BEC=∠BDC=90°,
又∵∠BOE=∠COD,
∴∠EBO=∠DCO,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形
【解析】首先可得∠OBC=∠OCB,证明∠EBO=∠DCO,继而可得∠ABC=∠ACB
【考点精析】根据题目的已知条件,利用等腰三角形的判定的相关知识可以得到问题的答案,需要掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目