题目内容
【题目】从⊙O外一点A引⊙O的切线AB,切点为B,连接AO并延长交⊙O于点C,点D.连接BC.
(1)如图1,若∠A=26°,求∠C的度数;
(2)如图2,若AE平分∠BAC,交BC于点E.求∠AEB的度数.

【答案】(1)∠C=32°;(2)45°.
【解析】试题分析:连接OB,根据切线的性质,得∠OBA=90°,又∠A=26°,所以∠AOB=64°,再用三角形的外角性质可以求出∠ACB的度数.
(2)由角平分线及三角形外角性质可得∠C+∠CAE=∠FBA+∠BAF,即∠BEF=∠BFE,再利用直径所对的圆周角是直角即可求解.
试题解析:(1)如图:连接OB,
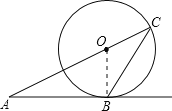
∵AB切⊙O于点B,
∴∠OBA=90°,
∵∠A=26°,
∴∠AOB=90°-26°=64°,
∵OB=OC,
∴∠C=∠OBC,
∵∠AOB=∠C+∠OBC=2∠ACB,
∴∠ACB=32°.
(2)如图,连接BD交AE于点F.
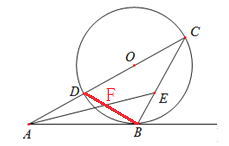
∵AB是⊙O的切线,
∴∠C=∠DBA.
又∵AE是∠CAB的平分线,
∴∠CAE=∠BAE,
∴∠C+∠CAE=∠ABD+∠BAE,
∴∠AEB=∠BFE.
∵CD是⊙O直径,
∴∠CBD=90°.
∴∠AEB=45°.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目