题目内容
【题目】如图所示,在□ABCD中,AE⊥BD , CF⊥BD , 垂足分别为点E , F , 点G、H分别为AD , BC的中点,试证明EF和GH互相平分.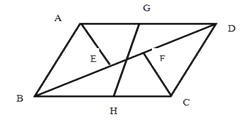
【答案】证明:设BD于GH交于O ,
∵四边形ABCD是平行四边形,
∴AD=BC , AD//BC
∴∠GDO=∠BHO , ∠GDO=∠HBO
∵G,H是AD , BC的中点 ,
∴DG=BH
∴△DGO≌△BHO ,
∴GO=HO , DO=BO ,
∵AE⊥BD , CF⊥BD ,
∴∠AED=∠CFB=90 ,
又∵∠ADE=∠CBF , AD=BC ,
∴△ADE≌△CBF ,
∴DE=BF ,
∴DE-DO=BF-BO ,
即EO=FO ,
∴EF和GH互相平分.
【解析】利用平行四边形的性质与判定证明△DGO≌△BHO , △ADE≌△CBF是本题的关键.
【考点精析】关于本题考查的平行四边形的判定,需要了解两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能得出正确答案.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目