题目内容
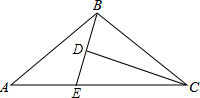
如图,点O是△ABC内一点,且OA=OB=OC,若∠OBA=20°,∠OCB=30°,则∠OAC=______.
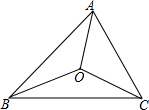

∵OA=OB=OC,∠OBA=20°,∠OCB=30°,
∴∠OAB=∠OBA=20°,∠OCB=∠OBC=30°,∠OAC=∠OCA,
∵在△ABC中,∠OAB+∠OBA+∠OAC+∠OCA+∠OCB+∠OBC=180°,
∴20°+20°+30°+30°+2∠OAC=180°,
∴∠OAC=40°,
故答案为:40°.
∴∠OAB=∠OBA=20°,∠OCB=∠OBC=30°,∠OAC=∠OCA,
∵在△ABC中,∠OAB+∠OBA+∠OAC+∠OCA+∠OCB+∠OBC=180°,
∴20°+20°+30°+30°+2∠OAC=180°,
∴∠OAC=40°,
故答案为:40°.

练习册系列答案
相关题目