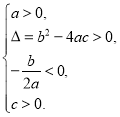题目内容
【题目】阅读下面材料:
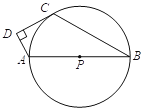
在数学课上,老师提出利用尺规作图完成下面问题:


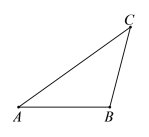
根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
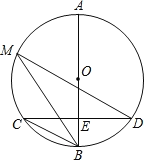
证明:连接OA,OB,OC,
由作图可知 OA=OB=OC( )(填推理的依据)
∴⊙O为△ABC的外接圆;
∵点C,P在⊙O上,![]()
∴∠APB=∠ACB.( )(填推理的依据)
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据作图语言画出对应的几何图形即可;
(2)根据线段垂直平分线的性质填写;根据圆周角定理的推论即得答案.
解:(1)符合题意的图形如图所示:
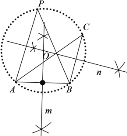
(2)证明:连接OA,OB,OC,
由作图可知 OA=OB=OC(线段垂直平分线上的点到这条线段两个端点的距离相等),
∴⊙O为△ABC的外接圆;
∵点C,P在⊙O上,![]() ,
,
∴∠APB=∠ACB(同弧所对的圆周角相等).
故答案为:线段垂直平分线上的点与这条线段两个端点的距离相等;同弧所对的圆周角相等.

【题目】关于x 的一元二次方程a x2 + bx + c = 0(a>0)有两个不相等且非零的实数根,探究a,b,c满足的条件.
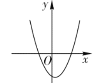
小华根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小华的探究过程:第一步:设一元二次方程ax2 +bx+c = 0(a>0)对应的二次函数为y = ax2 +bx +c(a>0);
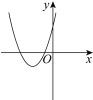
第二步:借助二次函数图象,可以得到相应的一元二次方程中a,b,c满足的条件,列表如下:
方程两根的情况 | 对应的二次函数的大致图象 | a,b,c满足的条件 |
方程有两个 不相等的负实根 |
|
|
①_______ |
|
|
方程有两个 不相等的正实根 | ②__________ | ③____________ |
(1)请帮助小华将上述表格补充完整;
(2)参考小华的做法,解决问题:
若关于x的一元二次方程![]() 有一个负实根和一个正实根,且负实根大于-1,求实数
有一个负实根和一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.