题目内容
如图,△ABC中,∠BAC=90°,AD⊥BC于D,若AB=2,BC=4,则CD的长是( )
| A.1 | B.4 | C.3 | D.2 |
C
解析试题分析:先由∠BAC=90°,AD⊥BC,∠B=∠B证得△ABD∽△CBA,再根据相似三角形的性质求得BD的长,即可求得结果.
解:∵∠BAC=90°,AD⊥BC,∠B=∠B
∴△ABD∽△CBA
∴
∵AB=2,BC=4
∴ ,解得
,解得
∴CD=BC-BD=3
故选C.
考点:相似三角形的判定和性质
点评:相似三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为
| A.10米 | B.12米 | C.15米 | D.22.5米 |
如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CE交AD于E,点F是AB的中点,则S△AEF:S四边形BDEF为
| A.3:4 | B.1:2 | C.2:3 | D.1:3 |
如图,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,则CD的长为
A. | B. | C.2 | D.3 |
如图,在 ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,
ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F, ,则DE:EC=【 】
,则DE:EC=【 】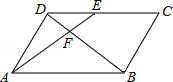
| A.2:5 | B.2:3 | C.3:5 | D.3:2 |


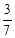



 B.
B.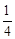 C.
C. D.
D.
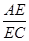 =
= ,则
,则 =________,BF=________.
=________,BF=________.