题目内容
如图，在△ABC中，BC＞AC，点D在BC上，且DC=AC，∠ACB的平分线CE交AD于E，点F是AB的中点，则S△AEF：S四边形BDEF为
| A．3：4 | B．1：2 | C．2：3 | D．1：3 |
D
解析试题分析：∵DC=AC，∴△ADC是等腰三角形。
∵∠ACB的平分线CE交AD于E，∴E为AD的中点（三线合一）。
又∵点F是AB的中点，∴EF为△ABD的中位线。
∴EF=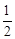
BD，△AFE∽△ABD。∴S△AFE：S△ABD=1：4。
∴S△AFE：S四边形BDEF=1：3。故选D。
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
已知△ABC∽△DEF，若△ABC与△DEF的相似比为3∶4，则△ABC与△DEF的面积比为( )
| A．4∶3 | B．3∶4 | C．16∶9 | D．9∶16 |
下列四个命题中，属于真命题的是
A．若 ，则a=m |
| B．若a＞b，则am＞bm |
| C．两个等腰三角形必定相似 |
| D．位似图形一定是相似图形 |
如图，△ABC中，∠BAC＝90°，AD⊥BC于D，若AB＝2，BC＝4，则CD的长是( )
| A．1 | B．4 | C．3 | D．2 |
