题目内容
在Rt△ABC和Rt△DEF中，∠ C=∠ F=90°，当AC=3，AB=5，DE=10，EF=8时，Rt△ABC和Rt△DEF是 的．（填“相似”或者“不相似”）
相似.
解析试题分析：首先利用勾股定理得出BC，DF的长，进而利用相似三角形的判定得出即可．
如图所示：∵AC=3，AB=5，DE=10，EF=8，
∴BC=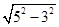
=4，DF=
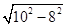=6，
∴AC:DF="CB:EF=1:2" ，
∵∠C=∠F=90°，
∴Rt△ABC∽Rt△DEF．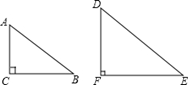
故答案为：相似．
考点：相似三角形的判定．
练习册系列答案
相关题目
如图，已知AB∥CD∥EF，那么下列结论正确的是（ ）
A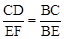． | B． | C． | D． |
如图，△ABC中，∠BAC＝90°，AD⊥BC于D，若AB＝2，BC＝4，则CD的长是( )
| A．1 | B．4 | C．3 | D．2 |
，
，
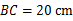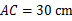，另一个与它相似的△
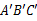的最短边长为45 cm，则△
中，
∥
，
，则
______．