题目内容
 如图,矩形ABCD,过对角线的交点O作OE⊥BC于E,连接DE交OC于O1,过O1作O1E1⊥BC于E1,连接DE1交OC于O2,过O2作O2E2⊥BC于E2,…,如此继续,可以依次得到点O3,O4,…,On,分别记△DOE,△DO1E1,△DO2E2,…,△DOnEn的面积为S1,S2,S3,…Sn-1.则Sn=________S矩形ABCD.
如图,矩形ABCD,过对角线的交点O作OE⊥BC于E,连接DE交OC于O1,过O1作O1E1⊥BC于E1,连接DE1交OC于O2,过O2作O2E2⊥BC于E2,…,如此继续,可以依次得到点O3,O4,…,On,分别记△DOE,△DO1E1,△DO2E2,…,△DOnEn的面积为S1,S2,S3,…Sn-1.则Sn=________S矩形ABCD.
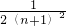
分析:根据矩形的性质推出△ABD≌△CDB,得到△ABD和△CBD的面积相等,且等于矩形面积的一半,根据等底等高的数据线的面积相等,求出S1,同理求出S2、S3,根据结果得出规律,即可求出答案.
解答:∵矩形ABCD,
∴∠DCB=90°,AD=BC,AB=CD,
∵BD=BD,
∴△ABD≌△CDB,
∴S△ABD=S△CBD=
 S矩形ABCD,
S矩形ABCD,∵矩形ABCD,
∴OB=OD,
∵OE⊥BC,∠DCB=90°,
∴OE∥CD,
∴BE=DE,
∴S△DBE=S△DEC=
 S△DBC,
S△DBC,∴S1=S△DOE=S△BOE=
 S△DBE=
S△DBE= S△DBC=
S△DBC= ×
× S平行四边形ABCD,
S平行四边形ABCD,∵BO=DO,BE=CE,OE∥CD,
∴
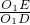 =
= =
= =
= ,
,同理:S2=
 ×
× ×
× S矩形ABCD=
S矩形ABCD= ×
× S矩形ABCD,
S矩形ABCD,S3=
 ×
× S矩形ABCD,
S矩形ABCD,…
SN=
 ×
×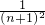 S矩形ABCD=
S矩形ABCD=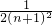 S矩形ABCD,
S矩形ABCD,故答案为:
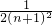 .
.点评:本题主要考查对三角形的面积,平行线分线段成比例定理,相似三角形的性质和判定,矩形的性质等知识点的理解和掌握,能求出三角形的面积并根据结果得出规律是解此题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 17、已知,如图,矩形ABCD中,AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F.
17、已知,如图,矩形ABCD中,AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F.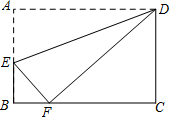 (2012•武汉)如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处.若AE=5,BF=3,则CD的长是( )
(2012•武汉)如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处.若AE=5,BF=3,则CD的长是( )
 Q的面积为y(cm2).
Q的面积为y(cm2). 如图,矩形ABCD的边AB、BC的长分别为
如图,矩形ABCD的边AB、BC的长分别为