Question

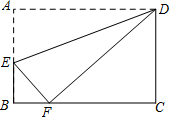（2012•武汉）如图，矩形ABCD中，点E在边AB上，将矩形ABCD沿直线DE折叠，点A恰好落在边BC的点F处．若AE=5，BF=3，则CD的长是（　　）

A．7

B．8

C．9

D．10

Answer 1

分析：先根据翻折变换的性质得出EF=AE=5，在Rt△BEF中利用勾股定理求出BE的长，再根据AB=AE+BE求出AB的长，再由矩形的性质即可得出结论．

解答：解：∵△DEF由△DEA翻折而成，
∴EF=AE=5，
在Rt△BEF中，
∵EF=5，BF=3，
∴BE=

EF2-BF2

=

52-32

=4，
∴AB=AE+BE=5+4=9，
∵四边形ABCD是矩形，
∴CD=AB=9．
故选C．

点评：本题考查的是图形的翻折变换，即折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．