题目内容
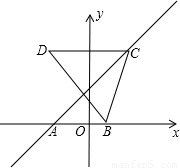
如图,直线y=x+2交x轴于点A,点C为直线y=x+2上一点,点D为点C关于y轴的对称点,点B(1,0).(1)求出点A的坐标.
(2)若点C的横坐标x=3,求点D的坐标.
(3)当∠BCD为直角时,直接写出△BCD的面积=______.
【答案】分析:(1)令y=0,求出x的值,即可得到点A的坐标;
(2)把点C的横坐标代入直线解析式求出纵坐标,得到点C的坐标,再根据关于y轴对称的点的横坐标互为相反数,纵坐标相等即可求出点D的坐标;
(3)根据∠BCD为直角可的点B、C的横坐标相同,然后求出点C的坐标,再求出点D的坐标,然后求出BC、CD的长,再利用三角形的面积公式列式计算即可得解.
解答:解:(1)令y=0,则x+2=0,
解得x=-2,
所以,A(-2,0);
(2)∵点C的横坐标x=3,
∴y=3+2=5,
∴点C的坐标为(3,5),
∵点D为点C关于y轴的对称点,
∴点D(-3,5);
(3)∵∠BCD为直角时,点D为点C关于y轴的对称点,
∴点B、C的横坐标相同,都是1,
∴y=1+2=3,
∴点C的坐标为(1,3),
∵点D为点C关于y轴的对称点,
∴点D的坐标为(-1,3),
∴BC=3,CD=1-(-1)=2,
∴△BCD的面积= BC•CD=
BC•CD= ×3×2=3.
×3×2=3.
故答案为:3.
点评:本题考查了两直线相交的问题,关于y轴对称的点的坐标的特征,三角形的面积,是基础题.
(2)把点C的横坐标代入直线解析式求出纵坐标,得到点C的坐标,再根据关于y轴对称的点的横坐标互为相反数,纵坐标相等即可求出点D的坐标;
(3)根据∠BCD为直角可的点B、C的横坐标相同,然后求出点C的坐标,再求出点D的坐标,然后求出BC、CD的长,再利用三角形的面积公式列式计算即可得解.
解答:解:(1)令y=0,则x+2=0,
解得x=-2,
所以,A(-2,0);
(2)∵点C的横坐标x=3,
∴y=3+2=5,
∴点C的坐标为(3,5),
∵点D为点C关于y轴的对称点,
∴点D(-3,5);
(3)∵∠BCD为直角时,点D为点C关于y轴的对称点,
∴点B、C的横坐标相同,都是1,
∴y=1+2=3,
∴点C的坐标为(1,3),
∵点D为点C关于y轴的对称点,
∴点D的坐标为(-1,3),
∴BC=3,CD=1-(-1)=2,
∴△BCD的面积=
 BC•CD=
BC•CD= ×3×2=3.
×3×2=3.故答案为:3.
点评:本题考查了两直线相交的问题,关于y轴对称的点的坐标的特征,三角形的面积,是基础题.

练习册系列答案
相关题目
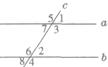 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )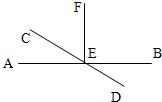 4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( )
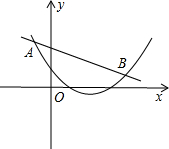
4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( )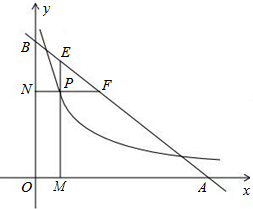 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数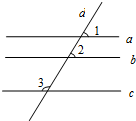 17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).
17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).