题目内容
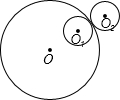 如图,⊙O的半径为r,⊙O1、⊙O2的半径均为r1,⊙O1与⊙O内切,沿⊙O内侧滚动m圈后回到原来的位置,⊙O2与⊙O外切并沿⊙O外侧滚动n圈后回到原来的位置,则m、n的大小关系是
如图,⊙O的半径为r,⊙O1、⊙O2的半径均为r1,⊙O1与⊙O内切,沿⊙O内侧滚动m圈后回到原来的位置,⊙O2与⊙O外切并沿⊙O外侧滚动n圈后回到原来的位置,则m、n的大小关系是
- A.m>n
- B.m=n
- C.m<n
- D.与r,r1的值有关
C
分析:设两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.
解答:大圆的半径为r,
则点O1运动所走过的圆的半径为r-r1,
点O2走过的圆的半径为r+r1.
根据圆的周长公式可知,
点O1运动所走过路程2π(r-r1)<点O2走过的过路程2π(r+r1),
所以m<n.
故选C.
点评:本题考查了由两圆位置关系来判断半径和圆心距之间数量关系的方法.
分析:设两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.
解答:大圆的半径为r,
则点O1运动所走过的圆的半径为r-r1,
点O2走过的圆的半径为r+r1.
根据圆的周长公式可知,
点O1运动所走过路程2π(r-r1)<点O2走过的过路程2π(r+r1),
所以m<n.
故选C.
点评:本题考查了由两圆位置关系来判断半径和圆心距之间数量关系的方法.

练习册系列答案
相关题目
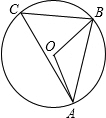 如图,⊙O的半径为5,AB=5
如图,⊙O的半径为5,AB=5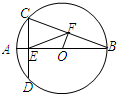 如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2=
如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2=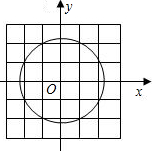 如图,⊙O的半径为
如图,⊙O的半径为 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.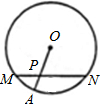 如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为
如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为