题目内容
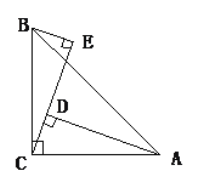
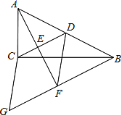
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的中线,过点
边上的中线,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 平行线,交
平行线,交![]() 的延长线于点
的延长线于点![]() ,在延长线上截得
,在延长线上截得![]() ,连结
,连结![]() 、
、![]() .若
.若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积等于________.
的面积等于________.
【答案】![]()
【解析】
首先可判断四边形CGFD是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形CGFD是菱形,CD∥BF,D为AB中点,E为AF的中点,得EF的长,设GF=x,则BF=11-x,AB=2x,在RT△ABF中利用勾股定理可求出x的值.
: ∵∠ACB=90°,CD为AB边上的中线,
∴AD=BD=CD,
∵BG∥CD,
∴AF⊥BG,
∴AD=BD=DF,
∴DF=CD,
∵FG=CD,
∴四边形CGFD为菱形,
∵CD∥BF,D为AB中点,
∴E为AF的中点,
∴EF=![]() AF=4,
AF=4,
设GF=x,则BF=11-x,AB=2x,
∵在RT△ABF中, ∠BFA=90°,
∴AF+BF=AB,即(11-x)+8=(2x),
解得:x=5或x=-![]() (舍去),
(舍去),
∴菱形CGFD的面积为:5×4=20,
故答案为:20.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共4只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
摸到白球的频率 | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
(1)请估计:当n很大时,摸到白球的频率将会接近 (精确到0.01);
(2)试估算口袋中白种颜色的球有多少只?
(3)请根据估算的结果思考从口袋中先摸出一球,不放回,再摸出一球,这两只球颜色不同的概率是多少?画出树状图(或列表)表示所有可能的结果,并计算概率.