Question

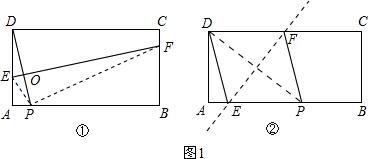
如图，在矩形ABCD中，AB=3，AD=1，点P在线段AB上运动，设AP=x，现将纸片折叠，使点D与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），再将纸片还原．
（1）当x=0时，折痕EF的长为______；当点E与点A重合时，折痕EF的长为______；
（2）请写出使四边形EPFD为菱形的x的取值范围，并求出当x=2时菱形的边长；
（3）令EF²=y，当点E在AD、点F在BC上时，写出y与x的函数关系式．当y取最大值时，判断△EAP与△PBF是否相似？若相似，求出x的值；若不相似，请说明理由．温馨提示：用草稿纸折折看，或许对你有所帮助哦！

Answer 1

解：（1）当x=0时，折痕EF=AB=3，当点E与点A重合时，折痕EF==．

（2）1≤x≤3．
当x=2时，如图，连接PE、PF．
∵EF为折痕，
∴DE=PE，
令PE为m，则AE=2-m，DE=m，
在Rt△ADE中，AD²+AE²=DE²
∴1+（2-m）²=m²，解得m=；
此时菱形边长为．

（3）如图2，过E作EH⊥BC；
∵△EFH∽△DPA，
∴，
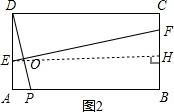
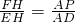∴FH=3x；
∴y=EF²=EH²+FH²=9+9x²；
当F与点C重合时，如图3，连接PF；

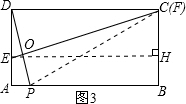
∵PF=DF=3，
∴PB=，
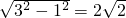∴0≤x≤3-2；
∵函数y=9+9x²的值在y轴的右侧随x的增大而增大，
∴当x=3-2时，y有最大值，
此时∠EPF=90°，△EAP∽△PBF．
综上所述，当y取最大值时△EAP∽△PBF，x=3-2．
分析：（1）当x=0时，点A与点P重合，则折痕EF的长等于矩形ABCD中的AB，当点E与点A重合时，折痕是一个直角的角平分线，可求EF=；
（2）由题意可知，EF垂直平分线段DP，要想使四边形EPFD为菱形，则EF也应被DP平分，所以点E必须要在线段AB上，点F必须在线段DC上，即可确定x的取值范围．再利用勾股定理确定菱形的边长．
（3）构造直角三角形，利用相似三角形的对应线段成比例确定y的值，再利用二次函数的增减性确定y的最大值．
点评：此题是一道综合性较强的题目，主要考查学生的图感，利用折叠过程中的等量关系寻找解题途径；特别是最后一问中涉及到的知识点比较多，需要同学们利用相似三角形的性质确定函数关系式后再根据自变量的取值范围来确定二次函数的最值问题．