题目内容
【题目】某服装店销售一种内衣,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x元/件的关系如表:
销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
(1)试求出y与x的之间的函数关系式;
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价的什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)服装店决定将一周的销售内衣的利润全部捐给福利院,在服装店购进该内衣的贷款不超过8000元情况下,请求出该服装店最大捐款数额是多少元?
【答案】(1)y=﹣10x+1000,(x≥50);(2)当40<x<70时,销售利润随着销售单价的增大而增大;(3)S=8000,即该商家最大捐款数额是8000元.
【解析】
试题分析:(1)设y=kx+b,把点的坐标代入解析式,求出k、b的值,即可得出函数解析式;
(2)根据利润=(售价﹣进价)×销售量,列出函数关系式,继而确定销售利润随着销售单价的增大而增大的销售单价的范围;
(3)根据购进该商品的贷款不超过8000元,求出进货量,然后求最大销售额即可.
解:(1)设y=kx+b,
由题意得,![]() ,
,
解得:![]() ,
,
则函数关系式为:y=﹣10x+1000,(x≥50)
(2)由题意得,S=(x﹣40)y=(x﹣40)(﹣10x+1000)
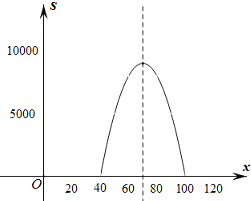
=﹣10x2+1400x﹣40000=﹣10(x﹣70)2+9000,
∵﹣10<0,
∴函数图象开口向下,对称轴为直线x=70,
∴当40<x<70时,销售利润随着销售单价的增大而增大;
(3)∵购进该商品的货款不超过8000元,
∴y的最大值为![]() =200(件).
=200(件).
由(1)知y随x的增大而减小,
∴x的最小值为:x=80,
由(2)知 当x≥70时,S随x的增大而减小,
∴当x=80时,销售利润最大,
此时S=8000,即该商家最大捐款数额是8000元.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案