题目内容
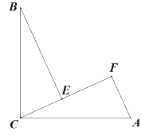
【题目】(1)思考探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数.
(2)类比探究:如图,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子表示).
(3)拓展迁移:已知,在四边形ABCD中,四边形ABCD的内角∠ABC与外角∠DCE的平分线所在直线相交于点P,∠P=n°,请画出图形;并探究出∠A+∠D的度数(用含n的式子表示).

【答案】(1)∠A=30°,∠P=15°;(2)∠A=2n°;(3)画图见解析;∠A+∠D=180°+2n°或180°﹣2n°.
【解析】
(1) 根据三角形内角和定理可以算出∠A的大小,再根据角平分线的性质和三角形的一个外角等于与它不相邻的两个内角的和可得∠PCD=∠P+∠PBC,即可得解;
(2)和(1)证明方法类似,先证明∠A+∠ABC=2(∠P+∠PBC),再证明∠A=2∠P即可得到答案;
(3) 延长BA交CD的延长线于F根据三角形内角和定理和三角形的一个外角等于与它不相邻的两个内角的和,即可得到第一种情况;延长AB交DC的延长线于F,同理即可得到答案.
解:(1)∠A=30°,∠P=15°
∵∠ACD+∠ACB=180°,∠ACD=100°
∴∠ACB=80°,
∵∠ABC+∠ACB+∠A=180°(三角形内角和定理),
又∵∠ABC=70°,
∴∠A=30°,
∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠PCD=![]() ∠ACD=50°,∠PBC=
∠ACD=50°,∠PBC=![]() ∠ABC=35°
∠ABC=35°
∵∠PBC+∠PCB+∠P=180°,∠PCB+∠PCD=180°
∴∠PCD=∠PBC+∠P
∴∠P=50°-35°=15°
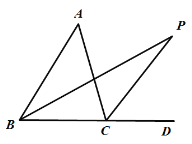
(2)结论:∠A=2n°,理由如下:
∵∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC(三角形的一个外角等于与它不相邻的两个内角和),
又∵P点是∠ABC和外角∠ACD的角平分线的交点,
∴∠ACD=2∠PCD,∠ABC=2∠PBC,
∴∠A+∠ABC=2(∠P+∠PBC)(等量替换),
∴∠A+∠ABC=2∠P+2∠PBC,
∴∠A+∠ABC=2∠P+∠ABC(等量替换),
∴∠A=2∠P;
∴∠A=2n°
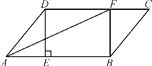
(3)(Ⅰ)如图②延长BA交CD的延长线于F.
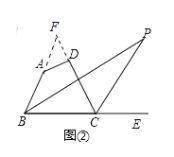
∵∠F=180°﹣∠FAD﹣∠FDA
=180°﹣(180°﹣∠A)﹣(180°﹣∠D)
=∠A+∠D﹣180°,
由(2)可知:∠F=2∠P=2n°,
∴∠A+∠D=180°+2n°。
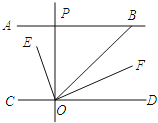
(Ⅱ)如图③,延长AB交DC的延长线于F.
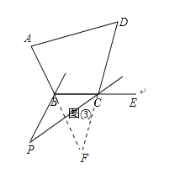
∵∠F=180°﹣∠A﹣∠D,∠P=![]() ∠F,
∠F,
∴∠P=![]() (180°﹣∠A﹣∠D)=90°﹣
(180°﹣∠A﹣∠D)=90°﹣![]() (∠A+∠D).
(∠A+∠D).
∴∠A+∠D=180°﹣2n°
综上所述:∠A+∠D=180°+2n°或180°﹣2n° ;

【题目】下表是加热食用油的温度变化情况:
时间 | 0 | 10 | 20 | 30 | 40 |
油温 | 10 | 30 | 50 | 70 | 90 |
王红发现,烧了110![]() 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )
A.没有加热时,油的温度是10℃B.加热50![]() ,油的温度是110℃
,油的温度是110℃
C.估计这种食用油的沸点温度约是230℃D.每加热10![]() ,油的温度升高30℃
,油的温度升高30℃
【题目】某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型 | 频数 | 频率 |
跳长绳 | 25 | a |
踢毽子 | 20 | 0.2 |
背夹球 | b | 0.4 |
拔河 | 15 | 0.15 |
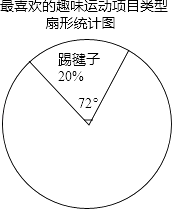
(1)直接写出a= , b=;
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?