题目内容
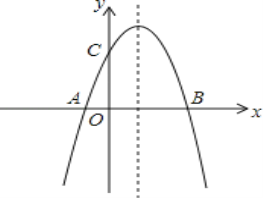
【题目】如图,已知抛物线![]() =
=![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式及顶点![]() 坐标;
坐标;
(2)在抛物线的对称轴上找到点![]() ,使得
,使得![]() 的周长最小,并求出点
的周长最小,并求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,若点![]() 是线段
是线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合).过点
重合).过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() .设
.设![]() 的长为
的长为![]() ,问当
,问当![]() 取何值时,
取何值时,![]() .
.
【答案】(1)![]() ,顶点
,顶点![]() 为
为![]() ;(2)
;(2)![]() ;(3)
;(3)![]() =
=![]() ,
,![]() =
=![]()
【解析】
(1)由点C的坐标,可求出c的值,再把![]() 、
、![]() 代入解析式,即可求出a、b的值,即可求出抛物线的解析式,将解析式化为顶点式,即可求出顶点
代入解析式,即可求出a、b的值,即可求出抛物线的解析式,将解析式化为顶点式,即可求出顶点![]() 的坐标;
的坐标;
(2)因为![]() 、
、![]() 关于抛物线的对称轴对称,连接
关于抛物线的对称轴对称,连接![]() 与抛物线对称轴交于一点,即为所求点
与抛物线对称轴交于一点,即为所求点![]() ,设对称轴与
,设对称轴与![]() 轴交于点
轴交于点![]() ,证明
,证明![]() ,即可求出
,即可求出![]() 的长,从而求出点P的 坐标;
的长,从而求出点P的 坐标;
(3)根据点A、B、M、C的坐标,可求出![]() ,从而求出
,从而求出![]() ,根据
,根据![]() =
=![]() ,
,![]() =
=![]() ,推出
,推出![]() =
=![]() ,因为
,因为![]() ,推出
,推出 ![]() =
=![]() ,从而得到
,从而得到![]() =
=![]() ,
,![]() ,根据
,根据![]() ,列出关于m的方程,解方程即可.
,列出关于m的方程,解方程即可.
(1)∵抛物线![]() =
=![]() 过
过![]() 、
、![]() ,
,![]() 三点,
三点,
∴![]() =
=![]() ,
,
∴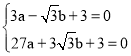 ,
,
解得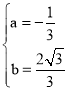 .
.
故抛物线的解析式为![]() ,
,
故顶点![]() 为
为![]() .
.
(2)如图![]() ,
,
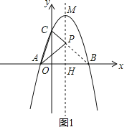
∵点![]() 、
、![]() 关于抛物线的对称轴对称,
关于抛物线的对称轴对称,
∴连接![]() 与抛物线对称轴交于一点,即为所求点
与抛物线对称轴交于一点,即为所求点![]() .
.
设对称轴与![]() 轴交于点
轴交于点![]() ,
,
∵![]() 轴,
轴,
∴![]() .
.
∴![]() .
.
由题意得![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() ,
,
∴![]() =
=![]() .
.
∴![]() .
.
(3)如图![]() ,∵
,∵![]() 、
、![]() ,
,![]() ,
,![]() ,
,
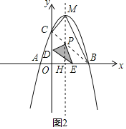
∴![]() =
=![]() .
.
∵![]() =
=![]() ,
,
∴![]() .
.
∵![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() .
.
∵![]() ,
,
∴![]() =
=![]() .
.
∴![]() =
=![]() ,
,![]() .
.
∵![]() =
=![]() ,
,
∴![]() =
=![]()
![]() .
.
∴![]() ,
,
解得![]() =
=![]() ,
,![]() =
=![]() .
.

练习册系列答案
相关题目
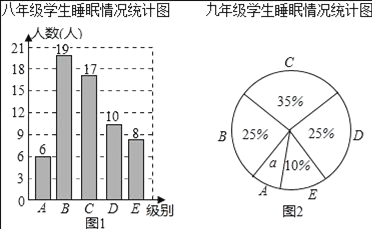
【题目】为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
组别 | 睡眠时间x(小时) |
|
|
|
|
|
|
|
|
|
|
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中![]() 的值 ;
的值 ;
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?