Question

如图，△ABC的高AD、BE相交于H，AD的延长线交过△ABC三个顶点的圆于F．求证：DH=FD．

Answer 1

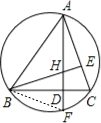证明：连接BF，
∵∠C=∠BFA，△ABC的高为AD、BE，
∴∠C+∠DAC=90°，∠AHE+∠CAD=90°，
∵∠AHE=∠DHB，
∠BHF+∠DAC=90°，
∴∠C=∠BHF，
∵∠BFA=∠BHF=∠C，
即∠BFA=∠BHF，
∴BH=BF，
又∵AD⊥BC，
∴HD=DF．
分析：连接BF，由圆周角定理得∠C=∠BFA，由△ABC的高AD、BE，可得出∠C=∠BHF，从而得出BH=BF，再由AD⊥BC，即可得出HD=FD．
点评：本题考查了圆周角定理，等边对等角，是基础知识要熟练掌握．解题的关键是发现同弧所对的圆周角之间的关系．