题目内容
 如图,△ABC的高AD=4,BC=8,四边形MNPQ是△ABC中任意一个内接矩形
如图,△ABC的高AD=4,BC=8,四边形MNPQ是△ABC中任意一个内接矩形(1)设MN=x,MQ=y,求y关于x的函数解析式;
(2)设MN=x,矩形MNPQ的面积为y,求y关于x的函数关系式,并求出当MN为多大时,矩形MNPQ面积y有最大值,最大值为多少?
分析:(1)由四边形MNPQ是△ABC中任意一个内接矩形,易证得△AMN∽△ABC,然后由相似三角形对应高的比等于相似比,即可求得y关于x的函数解析式;
(2)由(1),可求得MQ的值,然后由矩形的面积公式,即可求得y关于x的函数关系式,然后由二次函数的最值问题,求得当MN为多大时,矩形MNPQ面积y有最大值,最大值为多少.
(2)由(1),可求得MQ的值,然后由矩形的面积公式,即可求得y关于x的函数关系式,然后由二次函数的最值问题,求得当MN为多大时,矩形MNPQ面积y有最大值,最大值为多少.
解答:解:(1)∵四边形MNPQ是△ABC中一个内接矩形,
∴MN∥BC,MQ⊥BC,
∵AD⊥BC,
∴四边形MQDE是矩形,
∴MQ=DE,
∴△AMN∽△ABC,
∴
=
,
∵△ABC的高AD=4,BC=8,MN=x,MQ=y,
∴
=
,
解得:y=4-
x;
(2)∵由(1),可得MN=x,
∴MQ=4-
x,
∴y=S矩形MNPQ=MN•MQ=x(4-
x)=-
(x-4)2+8,
∵-
<0,
∴当MN为4时,矩形MNPQ面积y有最大值,最大值为8.
∴MN∥BC,MQ⊥BC,
∵AD⊥BC,
∴四边形MQDE是矩形,
∴MQ=DE,
∴△AMN∽△ABC,
∴
| AE |
| AD |
| MN |
| BC |
∵△ABC的高AD=4,BC=8,MN=x,MQ=y,
∴
| 4-y |
| 4 |
| x |
| 8 |
解得:y=4-
| 1 |
| 2 |
(2)∵由(1),可得MN=x,
∴MQ=4-
| 1 |
| 2 |
∴y=S矩形MNPQ=MN•MQ=x(4-
| 1 |
| 2 |
| 1 |
| 2 |
∵-
| 1 |
| 2 |
∴当MN为4时,矩形MNPQ面积y有最大值,最大值为8.
点评:此题考查了相似三角形的判定与性质、矩形的性质以及二次函数的性质.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
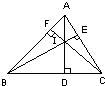 15、如图,△ABC的高AD、BE、CF相交于点I,△BIC的BI边上的高是
15、如图,△ABC的高AD、BE、CF相交于点I,△BIC的BI边上的高是 23、如图,△ABC的高BD、CE相交于点O,且OB=OC,AB与AC相等吗?为什么?
23、如图,△ABC的高BD、CE相交于点O,且OB=OC,AB与AC相等吗?为什么? 10、如图,△ABC的高AD、BE相交于点O,则∠C与∠BOD的关系是( )
10、如图,△ABC的高AD、BE相交于点O,则∠C与∠BOD的关系是( )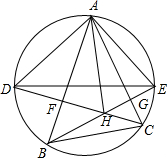 如图,△ABC的高CF、BG相交于点H,分别延长CF、BG与△ABC的外接圆交于D、E两点,则下列结论:①AD=AE;②AH=AE;③若DE为△ABC的外接圆的直径,则BC=AE.其中正确的是( )
如图,△ABC的高CF、BG相交于点H,分别延长CF、BG与△ABC的外接圆交于D、E两点,则下列结论:①AD=AE;②AH=AE;③若DE为△ABC的外接圆的直径,则BC=AE.其中正确的是( )