题目内容
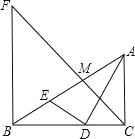
【题目】如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论①∠AED=∠ADC;②![]() ;③ACBE=12;④3BF=4AC,其中结论正确的个数有( )
;③ACBE=12;④3BF=4AC,其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】C.
【解析】
试题分析:①∠AED=90°﹣∠EAD,∠ADC=90°﹣∠DAC,∵∠EAD=∠DAC,
∴∠AED=∠ADC.故本选项正确;
②∵AD平分∠BAC,∴![]() ,∴设AB=4x,则AC=3x,
,∴设AB=4x,则AC=3x,
在直角△ABC中,AC2+BC2=AB2,则(3x)2+49=(4x)2,
解得:x=![]() ,
,
∵∠EAD=∠DAC,∠ADE=∠ACD=90°,
∴△ADE∽△ACD,得DE:DA=DC:AC=3:![]() ,故不正确;
,故不正确;
③由①知∠AED=∠ADC,
∴∠BED=∠BDA,
又∵∠DBE=∠ABD,
∴△BED∽△BDA,
∴DE:DA=BE:BD,由②知DE:DA=DC:AC,
∴BE:BD=DC:AC,
∴ACBE=BDDC=12.
故本选项正确;
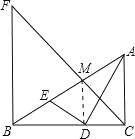
④连接DM,
在Rt△ADE中,MD为斜边AE的中线,
则DM=MA.
∴∠MDA=∠MAD=∠DAC,
∴DM∥BF∥AC,
由DM∥BF得FM:MC=BD:DC=4:3;
由BF∥AC得△FMB∽△CMA,有BF:AC=FM:MC=4:3,
∴3BF=4AC.
故本选项正确.
综上所述,①③④正确,共有3个.
故选C.

练习册系列答案
相关题目