题目内容
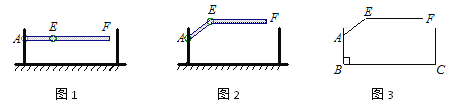
【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB如图,AB是
⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是弧AC的中点,⊙O的半径为1,求图中阴影部分的面积.
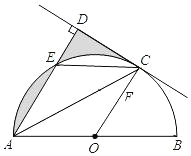
【答案】(1)CD与圆O相切;证明见解析
(2)S阴影=S△DEC=![]() ×
×![]() ×
×![]() =
=![]() .
.
【解析】
试题分析:(1)CD与圆O相切,理由如下:由AC为角平分线得到一对角相等,利用等角对等边得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到OC与AD平行,进而得到OC与CD垂直,即可得证;
(2)连接EB,交OC于F,利用直径所对的圆周角为直角,以及切线的性质,得到一对直角相等,利用同位角相等两直线平行得到OC与AD平行,由O为AB中点,得到F为BE中点,利用中位线定理求出OF的长,进而利用勾股定理求出EF的长,阴影部分面积等于三角形EDC面积,求出即可.
试题解析:(1)CD与圆O相切,理由如下:
∵AC为∠DAB的平分线,
∴∠DAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
则CD与圆O相切;
(2)连接EB,交OC于F,
∵AB为直径,
∴∠AEB=90°,
∴EB∥CD,
∵CD与⊙O相切,C为切点,
∴OC⊥CD,
∴OC∥AD,
∵点O为AB的中点,
∴OF为△ABE的中位线,
∴OF=![]() AE=
AE=![]() ,即CF=DE=
,即CF=DE=![]() ,
,
在Rt△OBF中,根据勾股定理得:EF=FB=DC=![]() ,
,
则S阴影=S△DEC=![]() ×
×![]() ×
×![]() =
=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车.已知过去两次租用这两种货车的情况如下表:
第一次 | 第二次 | |
甲种货车辆数(辆) | 2 | 5 |
乙种货车辆数(辆) | 3 | 6 |
累计运货吨数(吨) | 15.5 | 35 |
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问货主应付运费多少元?
【题目】在一次抽样调查中收集了一些数据,对数据进行分组,绘制了频数分布表,由于操作失误,绘制时不慎把第三小组的频数弄丢了,现在只知道最后一组(89.5~99.5)出现的百分比为15%,由此可知丢失的第三小组的频数是。
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~99.5 |
频数 | 9 | 15 | ? | 16 | 12 |