题目内容
【题目】如图,已知CF⊥AB于F,ED⊥AB于D,∠1=∠2,求证:FG∥BC.
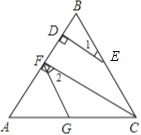
【答案】依题意知,CF⊥AB于F,ED⊥AB于D,∴∠BDE=∠BFC=90°,则DE∥FC,∴∠1=∠BCF。
∵∠1=∠2(已知)∴∠BCF=∠2.∴FG∥BC(内错角相等,两直线平行)
【解析】试题分析:根据在同一平面内垂直于同一条直线的两条直线平行可知DE∥FC,故∠1=∠ECF=∠2.根据内错角相等两直线平行可知,FG∥BC.
证明:∵CF⊥AB,ED⊥AB,
∴DE∥FC(垂直于同一条直线的两条直线互相平行),
∴∠1=∠BCF(两直线平行,同位角相等);
又∵∠2=∠1(已知),
∴∠BCF=∠2(等量代换),
∴FG∥BC(内错角相等,两直线平行).

练习册系列答案
相关题目