题目内容
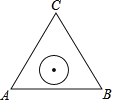
【题目】如图，若一个半径为1的圆形纸片在边长为6的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片能接触到的最大面积为_____．
【答案】6
+π．
【解析】
根据直角三角形的面积和扇形面积公式先求出圆形纸片不能接触到的面积，再用等边三角形的面积去减即可得能接触到的最大面积．
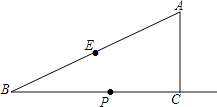
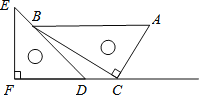
解：如图，
当圆形纸片运动到与∠A的两边相切的位置时，
过圆形纸片的圆心O作两边的垂线，垂足分别为D，E，
连接AO，
则Rt△ADO中，∠OAD＝30°，OD＝1，AD＝，
∴S△ADO＝
ODAD＝
，
∴S四边形ADOE＝2S△ADO＝，
∵∠DOE＝120°，
∴S扇形DOE＝
，
∴纸片不能接触到的部分面积为：
3（﹣）＝3﹣π
∵S△ABC＝×6×3＝9
∴纸片能接触到的最大面积为：
9﹣3+π＝6+π．
故答案为6+π．
练习册系列答案
相关题目
【题目】一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：
售价x（元/千克） | … | 50 | 60 | 70 | 80 | … |
销售量y（千克） | … | 100 | 90 | 80 | 70 | … |
（1）求y与x的函数关系式；
（2）该批发商若想获得4000元的利润，应将售价定为多少元？
（3）该产品每千克售价为多少元时，批发商获得的利润w（元）最大？此时的最大利润为多少元？
