题目内容
函数y=-ax+a与y=
(a≠0)在同一直角坐标系中的图象可能是( )
| a |
| x |
A.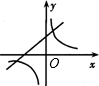 | B.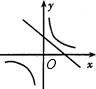 | C.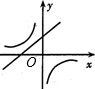 | D.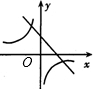 |
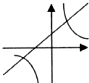
A、由一次函数y=-ax+a的图象y轴的正半轴相交可知-a>0,即a<0,与y=
(x≠0)的图象a>0相矛盾,故本选项错误;
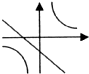
B、由一次函数y=-ax+a的图象y轴的正半轴相交可知-a<0,即a>0,与y=
(x≠0)的图象a>0一致,故本选项正确;
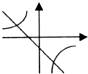
C、由一次函数y=-ax+a的图象与y轴的正半轴相交可知-a<0,即a>0,与y=
(x≠0)的图象a<0相矛盾,故本选项错误;
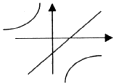
D、由一次函数y=-ax+a的图象可知a>0,与y=
(x≠0)的图象a<0相矛盾,故本选项错误.
故选B.
| a |
| x |
B、由一次函数y=-ax+a的图象y轴的正半轴相交可知-a<0,即a>0,与y=
| a |
| x |
C、由一次函数y=-ax+a的图象与y轴的正半轴相交可知-a<0,即a>0,与y=
| a |
| x |
D、由一次函数y=-ax+a的图象可知a>0,与y=
| a |
| x |
故选B.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目