题目内容
【题目】把一个函数图象上每个点的纵坐标变为原来的倒数(原函数图象上纵坐标为0的点除外)横坐标不变,可以得到另一个函数的图象,我们称这个过程为倒数变换.
例如:如图1,将y=x的图象经过倒数变换后可得到y=![]() 的图象.特别地,因为y=x图象上纵坐标为0的点是原点,所以该点不作变换,因此y=
的图象.特别地,因为y=x图象上纵坐标为0的点是原点,所以该点不作变换,因此y=![]() 的图象上也没有纵坐标为0的点.
的图象上也没有纵坐标为0的点.
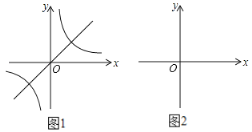
(1)请在图2中画出y=﹣x﹣1的图象和它经过倒数变换后的图象;
(2)观察上述图象,结合学过的关于函数图象和性质的知识.
①猜想:倒数变换得到的图象和原函数的图象之间可能有怎样的联系?写出两条即可.
②说理:请简要解释你其中一个猜想;
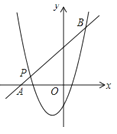
(3)设图2中的图象的交点为A,B,若点C的坐标为(﹣1,m),△ABC的面积为6,求m的值.
【答案】(1)见解析;(2)①猜想一:倒数变换得到的图象和原函数的图象之间如果存在交点,则其纵坐标为1或﹣1;猜想二:倒数变换得到的图象和原函数的图象的对称性相同,比如原函数是轴对称图形,则倒数变换的图象也是轴对称图象;②猜想一:说理见解析;(3)m=±6.
【解析】
(1)根据描点法画出y=﹣x﹣1的图象,并运用函数图象上每个点的纵坐标变为原来的倒数在平面直角坐标系中画出y=﹣x﹣1经过倒数变换后的图象.
(2)①猜想一:倒数变换得到的图象和原函数的图象之间如果存在交点,则其纵坐标为1或﹣1;猜想二:倒数变换得到的图象和原函数的图象的对称性相同,比如原函数是轴对称图形,则倒数变换的图象也是轴对称图象.
②进而利用只有1和﹣1的倒数是其本身,所以如果原函数存在一个点的纵坐标为1或﹣1,分析即可.
(3)联立两个函数关系式求得A,B点的坐标,将点C的坐标为(﹣1,m)代入△ABC的面积列出含m的代数表达式并使得值为6,进而求出m.
解:(1)在平面直角坐标系中画出y=﹣x﹣1的图象和它经过倒数变换后的图象如图:

图中去掉(﹣1,0)的点;
(2)①猜想一:倒数变换得到的图象和原函数的图象之间如果存在交点,则其纵坐标为1或﹣1;
猜想二:倒数变换得到的图象和原函数的图象的对称性相同,比如原函数是轴对称图形,则倒数变换的图象也是轴对称图象;
②猜想一:因为只有1和﹣1的倒数是其本身,所以如果原函数存在一个点的纵坐标为1或﹣1,那么倒数变换得到的图象上必然也存在这样对应的纵坐标为1或﹣1,即两个函数图象的交点.
(3)解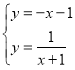 得
得![]() 或
或![]() ,
,
∴A(﹣2,1),B(0,﹣1),
∵C(﹣1,m),
∴S△ABC=![]() |m|×2=6,
|m|×2=6,
解得|m|=6,
∴m=±6.

 口算题天天练系列答案
口算题天天练系列答案【题目】为了创建文明城市,增强学生的环保意识.随机抽取8名学生,对他们的垃圾分类投放情况进行调查,这8名学生分别标记为![]() ,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
学生 垃圾类别 |
|
|
|
|
|
|
|
|
厨余垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
可回收垃圾 | √ | × | √ | × | × | √ | √ | √ |
有害垃圾 | × | √ | × | √ | √ | × | × | √ |
其他垃圾 | × | √ | √ | × | × | √ | √ | √ |
(1)求8名学生中至少有三类垃圾投放正确的概率;
(2)为进一步了解垃圾分类投放情况,现从8名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果.