题目内容
已知正比例函数y=kx与反比例函数y=
的图象都过A（m，1），则k=
．
| 3 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
分析：首先根据图象上点的坐标性质得出A点坐标，进而根据A点在y=kx上求出k的值即可．
解答：解：∵反比例函数y=
的图象过A（m，1），
∴1=
，
解得：m=3，
∴A点坐标为：（3，1），
∴代入y=kx得：
1=3k，
解得：k=
．
故答案为：
．
| 3 |
| x |
∴1=
| 3 |
| m |
解得：m=3，
∴A点坐标为：（3，1），
∴代入y=kx得：
1=3k，
解得：k=
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：此题主要考查了反比例函数与一次函数的交点问题，根据图象上点的坐标性质得出A点坐标是解题关键．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
已知正比例函数y=k1x（k1≠0）与反比例函数y=
（k2≠0）的图象有一个交点的坐标为（-2，-1），则它的另一个交点的坐标是（ ）
| k2 |
| x |
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
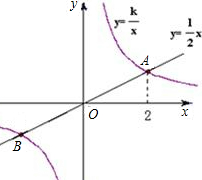横坐标为2．
如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．