��Ŀ����
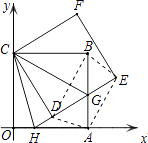
����Ŀ����ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��6��6������������ABCO�Ƶ�C��ʱ����ת�ǶȦ���0�㣼����90�㣩���õ�������CDEF��ED���߶�AB�ڵ�G��ED���ӳ��߽��߶�OA�ڵ�H����CH��CG��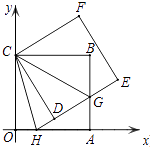
��1����֤����CBG�ա�CDG��
��2�����HCG�Ķ��������ж��߶�HG��OH��BG֮���������ϵ��˵�����ɣ�
��3������BD��DA��AE��EB�õ��ı���AEBD������ת�����У���G���ں�λ��ʱ�ı���AEBD�Ǿ��Σ���˵�����ɲ������H�����꣮
���𰸡�
��1��
֤�����߽�������ABCO�Ƶ�C��ʱ����ת�ǶȦ���
��DC=CO����CDG=��COA=90�㣬
���ı���OCBA�������Σ�
��CB=CO����B=90�㣬
��CB=CD����B=��CDG=90��
��Rt��CDG��Rt��CBG��
![]() ��
��
��Rt��CDG��Rt��CBG
��2��
�⣺�ߡ�CDG=90�㣬
���CDH=90�㣬
��Rt��COH��Rt��CDH��
![]() ��
��
��Rt��COH��Rt��CDH��
���OCH=��DCH��HO=DH��
��Rt��CDG��Rt��CBG��
���DCG=��BCG��DG=BG��
���HCG=��DCG+��DCH=45�㣬
HG=HD+DG=HO+BG
��3��
�⣺��G��AB�е�ʱ���ı���ADBE�Ǿ��Σ�
��G��AB�е㣬
��BG=AG= ![]() AB
AB
�ɣ�2����DG=BG��
�֡�AB=DE��
��DG= ![]() DE��
DE��
��DG=GE=BG=AG��
���ı���AEBD��ƽ���ı��Σ�
��AB=DE��
���ADBE�Ǿ��Σ�
���H��������x��0����
��HO=HD=x��DG=BG=AG=3��AH=6��x��
�ɹ��ɶ����ã���6��x��2+33=��3+x��2��
��ã�x=2��
��H��2��0����
����������1��������ת�任�����ʵõ�DC=CO����CDG=��COA=90�㣬���������ε����ʵõ�CB=CO����B=90�㣬����ֱ�������ε�ȫ�ȵ��ж�����֤�����ɣ���2��֤��Rt��COH��Rt��CDH���õ���OCH=��DCH��HO=DH�������������ɣ���3�����ݾ��ε��ж�����֤���ı���AEBD�Ǿ��Σ����H������Ϊ��x��0�������ݹ��ɶ����г����̣��ⷽ�����x��ֵ���õ���H�����꣮

 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�