题目内容
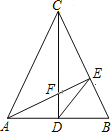
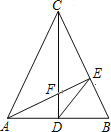
【题目】△ABC中，CA=CB，CD是中线，AE⊥BC于E交CD于F，求证：①△CBD∽△AFD，②DE2=DFDC．
【答案】见解析
【解析】
试题分析：（1）利用∠DAF=∠DCB和∠ADF=∠CDB，即可得出△ADE∽△FDB；
（2）由△ADF∽△CDB，可得
=
，再由DE是Rt△ABE斜边上的中线，得出DA=DB=DE，即可得出DE2=DCDF．
解：（1）∵△ABC中，CA=CB，CD是中线，
∴CD⊥AB，
∴∠ADF=∠CDB=90°，
又∵AE⊥BC，∠ABE=∠CBD，
∴∠DAF=∠DCB，
∴△CBD∽△AFD；
（2）∵△ADF∽△CDB，
∴=
，即DBDA=DFDC，
又∵DE是Rt△ABE斜边上的中线，
∴DA=DB=DE，
∴DE2=DCDF．
练习册系列答案
相关题目
