��Ŀ����
����Ŀ�����Ķ����ٻش����⣺
Ҫ�Ƚϴ���ʽA��B�Ĵ�С����������A-B���Ƚϲ��ȡֵ����A-B>0ʱ����A>B����A-B=0ʱ����A=B����A-B<0ʱ����A<B.�����磬��a<0ʱ���Ƚ�![]() �Ĵ�С.���Թ۲�
�Ĵ�С.���Թ۲�![]() ��Ϊ��a<0ʱ��-a>0�����Ե�a<0ʱ��
��Ϊ��a<0ʱ��-a>0�����Ե�a<0ʱ�� ![]() .
.
��1����֪M=![]() ,�Ƚ�M��N�Ĵ�С��ϵ.
,�Ƚ�M��N�Ĵ�С��ϵ.
��2��ij�ֲ�Ʒ��ԭ�����,������Ҿ������ڲ�Ʒ�������,�������ַ���:
����1����һ�����p%,�ڶ������q%;
����2����һ�����q%,�ڶ������p%;
����3����һ��������۾�Ϊ![]()
�����ԭ��ΪaԪ�����ú�a��p��q��ʽ�ӱ�ʾ��ۺ����ַ����ļ۸�.
����1�� ������2�� ������3��_______
���p,q�Dz���ȵ�����,���ַ�������������?
���𰸡���1����x>0ʱ�� M<N����x<0ʱ�� M>N����x=0ʱ�� M=N��
��2������1��a(1+m)(1+n)=a(1+m+n+mn)
����2��a(1+m)(1+n)=a(1+m+n+mn)
����3�� 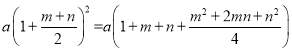
����3������
�������������������1������Ƚϼ��ɣ�
��2�����ݸ������е���۰ٷ��ʣ��ֱ��ʾ����ۺ�ĵ��ۣ��õ�����1��a��1+p����1+q��������2��a��1+q����1+p��������3��a��1+![]() ��2������1��2��Ȼ��ͬ���÷���3�ĵ��ۼ�ȥ����1�ĵ��ۣ���ȡa��������ȫƽ����ʽ������ʽ���Զ���ʽ�ķ���ȥ���źϲ�����������ȫƽ����ʽ���Σ�����p������q�ж������Ϊ�������ɵó�a��1+
��2������1��2��Ȼ��ͬ���÷���3�ĵ��ۼ�ȥ����1�ĵ��ۣ���ȡa��������ȫƽ����ʽ������ʽ���Զ���ʽ�ķ���ȥ���źϲ�����������ȫƽ����ʽ���Σ�����p������q�ж������Ϊ�������ɵó�a��1+![]() ��2��a��1+q����1+p��������ȷ��������3����۶࣮
��2��a��1+q����1+p��������ȷ��������3����۶࣮
�����������1����M=(x-2)(x-16)=x2-18x+32,
N=(x-4)(x-8)=x2-12x+32
��M-N=-6x
��x>0ʱ��-6x<0,M<N
![]()
![]()
��2������1��a(1+p%)(1+q%)��
����2��a(1+p%)(1+q%)��
����3�� ![]()
��p%=m,q%=n,����ۺ����ַ����ļ۸�ֱ�Ϊ
����1��a(1+m)(1+n)=a(1+m+n+mn)
����2��a(1+m)(1+n)=a(1+m+n+mn)
����3�� 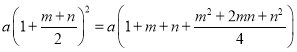
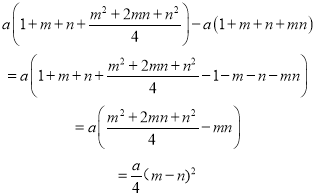
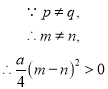
���Է���3������

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�