题目内容
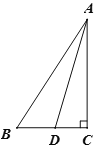
【题目】如图,Rt△ ABC中,∠ACB=90°,AD平分∠BAC, 作AD的垂直平分线EF交AD于点E,交BC的延长线于点F,交AB于点G,交AC于点H.
(1)依题意补全图形;
(2)求证:∠BAD=∠BFG;
(3)试猜想AB,FB和FD之间的数量关系并进行证明.
【答案】(1)补图见解析;(2)证明见解析;(3)![]() ,证明见解析.
,证明见解析.
【解析】
(1)根据题意补全图形;
(2)根据角平分线的定义得到∠BAD=∠CAD.在Rt△AEH和Rt△CFH中,根据三角形内角和定理得到∠CFH=∠CAD,等量代换即可得到结论;
(3)由线段垂直平分线的性质得到AF=FD,通过证明∠BAF=90°.在Rt△BAF中,利用勾股定理即可得到结论.
(1)补全图形如图;
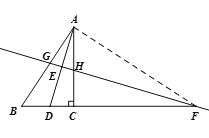
(2)∵AD平分∠BAC,∴∠BAD=∠CAD.
∵FE⊥AD,∠ACF=90°,∠AHE=∠CHF,∴∠CFH=∠CAD,∴∠BAD=∠CFH,即∠BAD=∠BFG.
(3)猜想:![]() .证明如下:
.证明如下:
连接AF.
∵EF为AD的垂直平分线,∴AF=FD,∠DAF=∠ADF,∴∠DAC+∠CAF=∠B+∠BAD.
∵AD是角平分线,∴∠BAD=∠CAD,∴∠CAF=∠ B,∴∠BAF=∠BAC+∠CAF=∠BAC+∠B=90°,∴![]() ,∴
,∴![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目